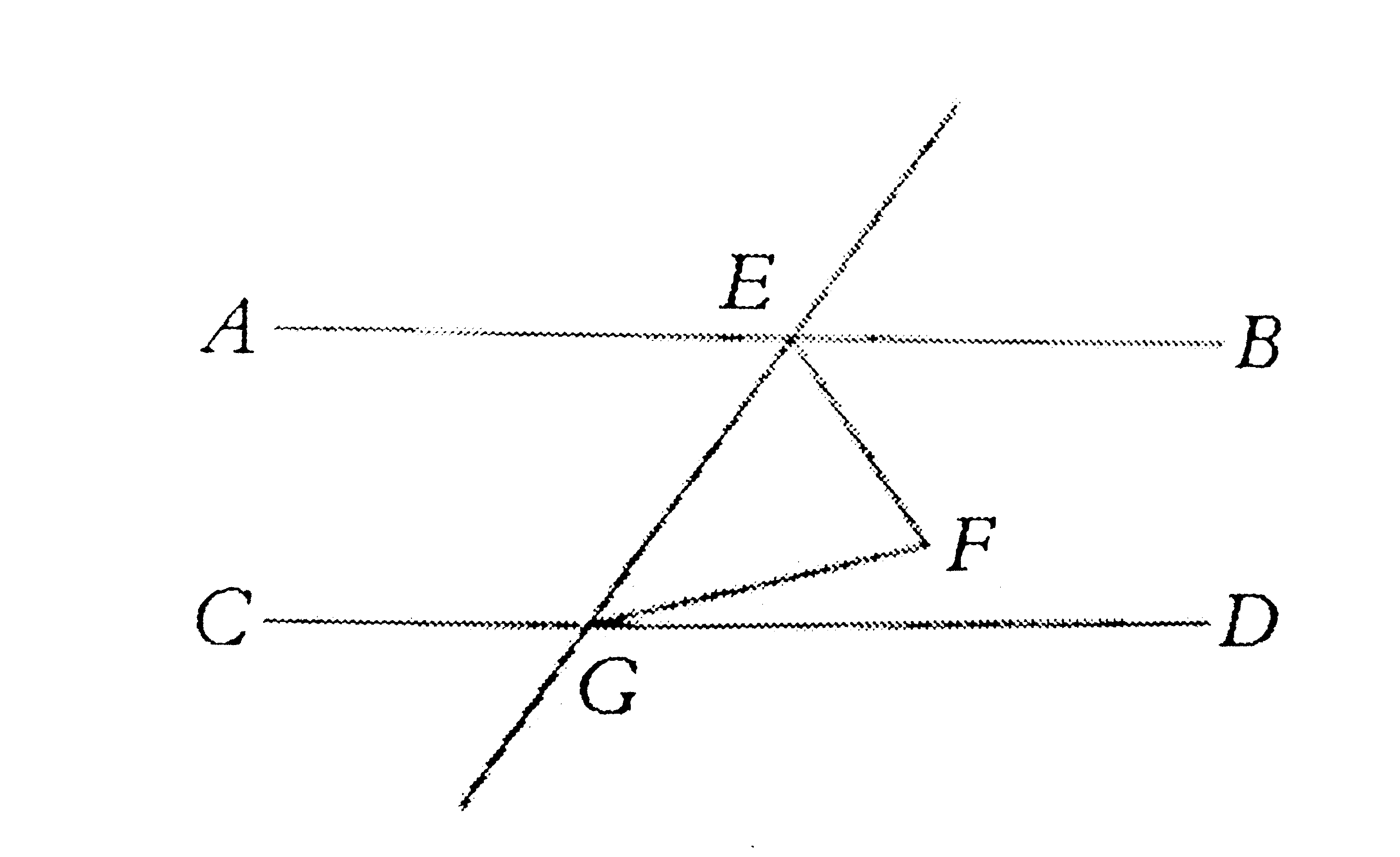
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.
A
20∘
B
25∘
C
40∘
D
35∘
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video, text & image solution for In the figure above, AB || CD. EF and FG are the bisectors of angleBEG and angleDGE, respectively. angleFEG=angleFGE+10^(@). Find angleFGE. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check

In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.A20∘B25∘C40∘D35∘In the figure , AB||CD, EG & FG are Bi sectors of ∠BEF & ∠DFE respectively , the m∠FGE is -
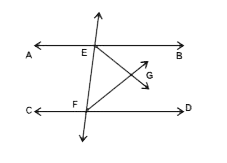 A45∘B90∘C60∘D100∘
A45∘B90∘C60∘D100∘
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘
In the given figure AB||CD and EF||DQ. Find the value of ∠DEF.
View SolutionIn the given figure AB||CD||EF then find the value of x
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
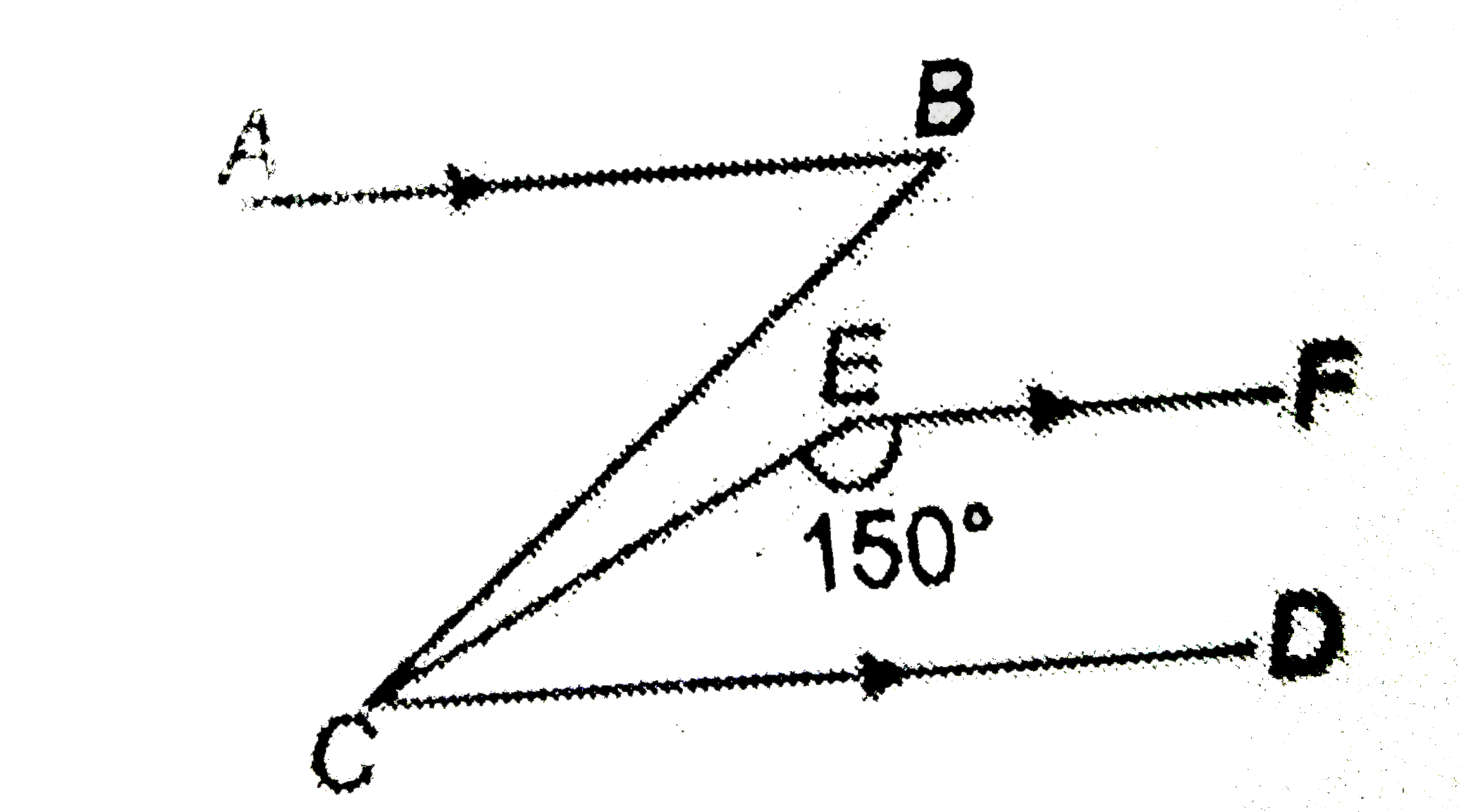
View SolutionIn the given figure AB||CDandEF||DQ. Find the value of ∠DEF:
View SolutionThe straight lines AB and CD intersect at E . If EF and EG are bisectors of ∠DEAand∠AEC respectively and if ∠AEF=xand∠AEG=y , then
View Solution

