The moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?Solution in Gujrati
1
3√2
√32
√32
The correct Answer is:C
I=ml212+mR24
or 1=m4(l33+R2) .....(1)
Also m=πR2lp
⇒R2=mπlp Put in equation (1)
I=m4(l23+mπlp)
For maxium & minima
dIdl=m4(2l3−mπl2p)=0
⇒2l3=mπl2p⇒2l3=πR2lpπl2p
or 2l3=R2l⇒lR=√32
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 3
92 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
The diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
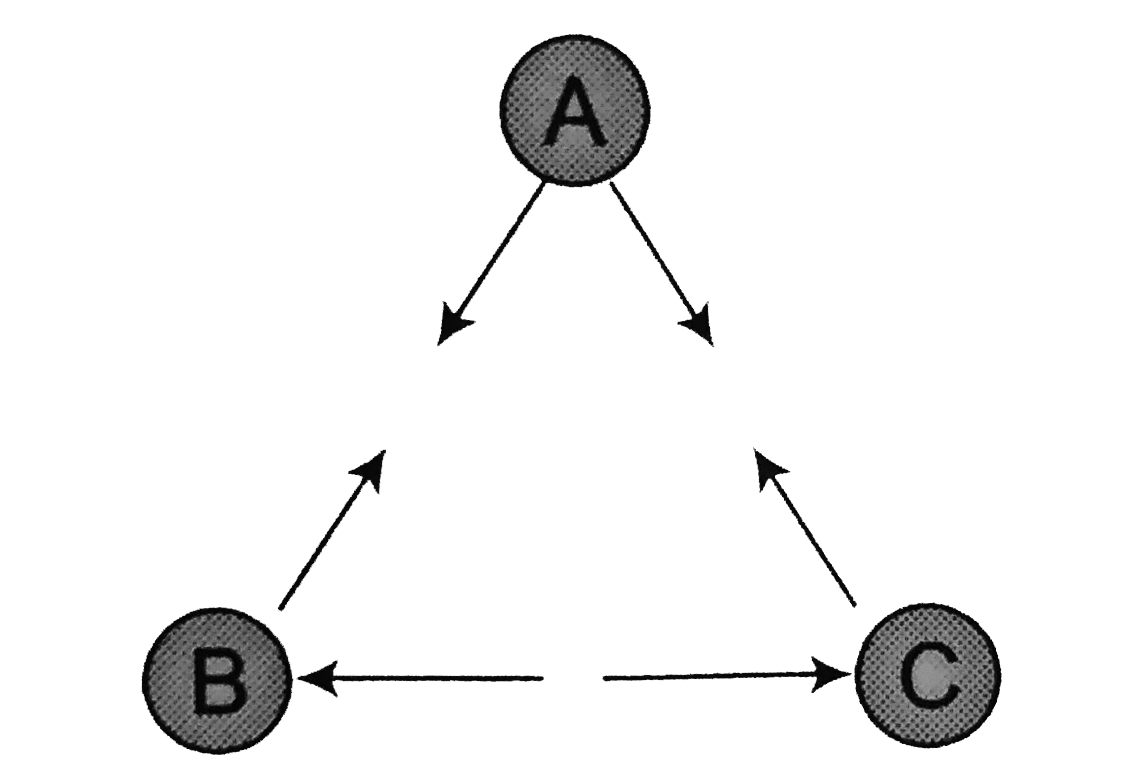
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionWhat is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View SolutionThe moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is I . What is the ratio l//R such that the moment of inertia is minimum ?
View Solutionलम्बाई l तथा त्रिज्या R के एक ठोस बेलन का अपनी ज्यामितीय अक्ष के परितः जड़त्व-आघूर्ण उतना ही है जितना कि निरक्षीय अक्ष के परितः है। R तथा l का अनुपात है
View Solutionएक त्रिज्या R तथा लम्बाई l के एकसमान बेलन का उसके अभिलम्ब द्विभाजक के सापेक्ष जड़त्व आघूर्ण I है। जड़त्व आघूर्ण के निम्नतम मान के लिए अनुपात l/R क्या होगा?
View Solutionत्रिज्या R तथा लम्बाई L के एकसमान बेलन का उसके अभिलम्ब द्विभाजक के सापेक्ष जड़त्व आघूर्ण है। जड़त्व आघूर्ण के निम्नतम मान के लिये अनुपात L/R होगा ?
View SolutionThe moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is I. What is the ratio lR such that the moment of inertia is minimum ?
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View Solutionएक बेलन की त्रिज्या R तथा लम्बाई L है। यदि इसके केन्द्र तथा इसके वृत्ताकार सतह के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण, उसके केन्द्र व लम्बाई के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण बराबर हों, तो
View SolutionThe moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is l. What is the ratio IR such that moment of inertia is minimum ?
View SolutionWhat is moment of inertia of uniform rod of mass M and length L about its perpendicular bisector
View Solutionएक ठोस बेलन का द्रव्यमान M लम्बाई L तथा त्रिज्या R है। इस बेलन का जड़त्व-आघूर्ण उसके किसी जनित्र के परितः क्या है।
View Solutionएक बेलन जिसका द्रव्यमान M, लम्बाई L तथा त्रिज्या R हैं। यदि इसका जड़त्व आघूर्ण, इसके केन्द्र से जाने वाले तथा इसके केन्द्र के लम्बवत् अक्ष के परित: न्यूनतम है, तब अनुपात L/R बराबर है
View Solution
