एक बेलन जिसका द्रव्यमान M, लम्बाई L तथा त्रिज्या R हैं। यदि इसका जड़त्व आघूर्ण, इसके केन्द्र से जाने वाले तथा इसके केन्द्र के लम्बवत् अक्ष के परित: न्यूनतम है, तब अनुपात L/R बराबर है
3/2
2/3
√2/3
√3/2
The correct Answer is:D
बेलन का जड़त्व आघूर्ण बेलन के अक्ष के लम्बवत्, तथा इसके केन्द्र से जाने वाले अक्ष के परितः
l=M(R24+L212) ....(i)
यदि ρ बेलन का आयतन घनत्व है, तब
M=(πR2L)ρ= नियतांक ….(ii)
∴L=MπR2ρ
समी (i) में रखने पर
l=M(R24+M212π2R4ρ4)
l के न्यूनतम होने के लिए, dldR=0
dldR=M(R2−M23π2R5)=0
R2=M23π2ρ2R5
या R6=2M23π2ρ2
समी (ii) से, R6=2π2R4L2ρ23π2ρ2
या R2=23L2 या L2R2=32 या LR=√3/2
Topper's Solved these Questions
- घूर्णन गति Book:ARIHANT HINDIChapter:घूर्णन गति Exercise:प्रश्नावली स्तर 2 प्रश्नावली एक या एक से अधिक विकल्प सही हैं
Explore 6 Videos
- घूर्णन गति Book:ARIHANT HINDIChapter:घूर्णन गति Exercise:प्रश्नावली स्तर 2 (शृंखलाबद्ध-बाधन प्रकार) अनुच्छेद-I
Explore 5 Videos
- घूर्णन गति Book:ARIHANT HINDIChapter:घूर्णन गति Exercise:प्रश्नावली स्तर 1
Explore 64 Videos
- घूर्णन Book:ARIHANT HINDIChapter:घूर्णन Exercise:प्रश्नावली (विगत वर्षो के प्रश्न)
Explore 22 Videos
- ठोस एवं अर्ध्दचालक युक्तियाँ Book:ARIHANT HINDIChapter:ठोस एवं अर्ध्दचालक युक्तियाँ Exercise:प्रश्नावली स्तर 2 विगत वर्षों के प्रशन
Explore 9 Videos
Similar Questions
साइकिल का एक पहिया एक खुरदी सड़क पर बिना फिसले एक रेखीय चाल से चित्रानुसार चलता है, तब
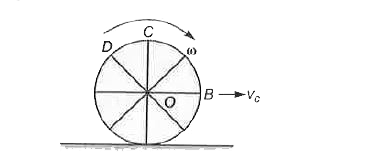
View Solutionघूर्णन गति की तीन समीकरणे ω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v=rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
घड़ी की मिनट वाली सुईं की कोणीय चाल है
View Solutionकिसी एकसमान वृत्तीय चकती का इसके व्यास के परितः जड़त्व आघूर्ण I है। इसके तल के लम्बवत् एवं इसकी परिधि के एक बिन्दु से होकर गुजरने वाली अक्ष के परितः इसका जड़त्व आघूर्ण होगा
View Solutionएक द्विपरमाणुक अणु m1 तथा m2 के दो द्रव्यमानो से बना है जोको दूरी r पर है यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकार हम इसकी घूर्णन ऊर्जा की गणना करें तब इसकी ऊर्जा दी जाएगी (n एक पूर्णांक है)
View SolutionOR गेट के निर्गत को NAND गेट के दोनों निवेशों से जोड़ा जाता है। संयोजन इस भाँति कार्य करेगा
View Solutionसिद्ध कीजिए कि y2+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अक्ष x-अक्ष के समांतर है। इसका शीर्ष तथा इसके नाभिलम्ब का समीकरण ज्ञात कीजिए।
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionएक स्थिर आयतन वाले खुले टैंक का आधार वर्गाकार है। यदि अंत: पृष्ठ न्यूनतम हो, तब टैंक कि गहराई तथा लम्बाई का अनुपात ज्ञात कीजिए।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution

