State the condition of total internal reflectoin to take place at an interface separating two transparent media. Hence derive the expression for the critical angle in terms of speed of light in two media.Solution in Punjabi
Step by step video solution for State the condition of total internal reflectoin to take place at an interface separating two transparent media. Hence derive the expression for the critical angle in terms of speed of light in two media. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A ray of light while travelling from a denser to a rarer medium undergoes total internal reflection. Derive the expression for the critical angle in terms of the speed of light in the respective media.
View SolutionWhen a ray of monochromatic light is incident obliquely on the interface of two media,
View SolutionDerive an expression for refraction at a single spherical surface OR A spherical surface separates two transparent media. Derive an expression that relates object and image distances with the radius of curvature for a point object. Clearly state the assumptions, if any.
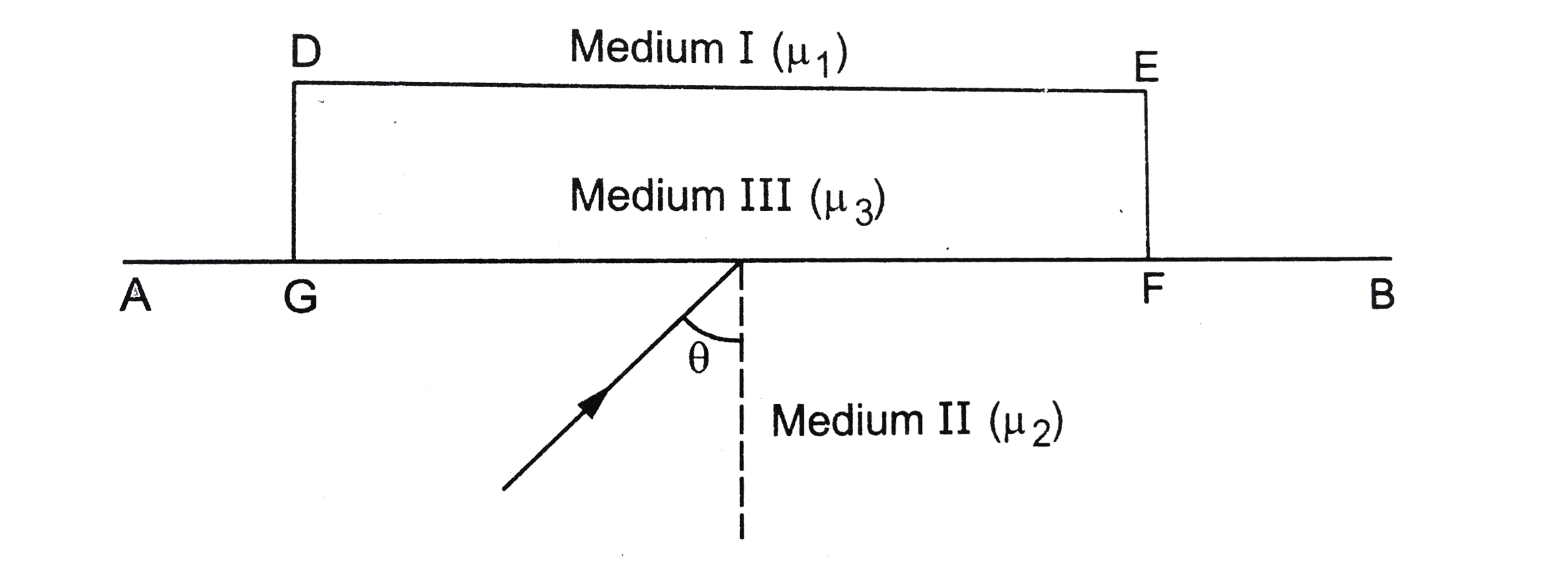
View SolutionMonochramatic light is incident on the pLane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
View SolutionTwo refracting media are separated by a spherical interface as shown in the figure.
View SolutionTwo transparent media A and B are separated by a plane boundary. The speed of light in medium A is 2.0×108ms−1 and in medium B is 2.5×108ms−1. The critical angle for which a ray of light going from A to B suffers total internal reflection is
View SolutionA ray is incident on interface of two media at critical angle as shown in the figure.
View SolutionTwo transparent media A and B are separated by a plane boundary. The speed of light are 2 times 10^(-8) m/s and 2.4 times 10^(-8) m/s respectively in A and B. Then the critical angle for a ray of light for these two media is
View Solution
