A wire of mass 9.8⋅10−3kg per metre passes over a friction less pulley fixed on the top of an inclined friction less plane which makes an angle of 30∘ with the horizontal. Masses M1 and M2 are tied at the two end of the wire. The mass M1 rests on the plane and the mass M2 hangs vertically downward. The whole system is in equilibrium. Now a transverse wave propagates along the wire with a velocity of 100ms−1. Find the values of masses M1 and M2. Take g= 9.8ms−2.Solution in Punjabi
Step by step video & image solution for A wire of mass 9.8*10^(-3)kg per metre passes over a friction less pulley fixed on the top of an inclined friction less plane which makes an angle of 30^@ with the horizontal. Masses M_(1) and M_(2) are tied at the two end of the wire. The mass M_(1) rests on the plane and the mass M_(2) hangs vertically downward. The whole system is in equilibrium. Now a transverse wave propagates along the wire with a velocity of 100ms^(-1). Find the values of masses M_(1) and M_(2). Take g= 9.8ms^(-2). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Can mechanical waves travel through vacuum?
View SolutionDefine unit
View SolutionWhat is the work done in holding a 15 kg suitcase whiel waiting for a bus for 15 mimnutes?
View SolutionTwo blocks of masses m_(1) and m_(2) are connected through a massless inextensible string .A block of mass m_(1) is placed at the fixed rigid inclined surface while the block of mass m_(2) hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m_(1) and m_(2) released from rest
View SolutionA wire of mass 9.8 xx 10^(-3) kg per metre passes over a frictionless pulley fixed on the top of an inclined frictionless plane which makes an angle of 30^(@) with the horizontal Masses M_(1) and M_(2) are tied at the two ends of the wire The mass M_(1) rests on the plane and mass M_(2) hangs freely vertically downwards . The whole systemis in equilibrium Now a transverse wave propagates along the wire with a velocity of 100 m//s If g = 9.8 m//s^(2) calculate the valuse of masses M_(1) and M_(2) .
View SolutionTwo masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
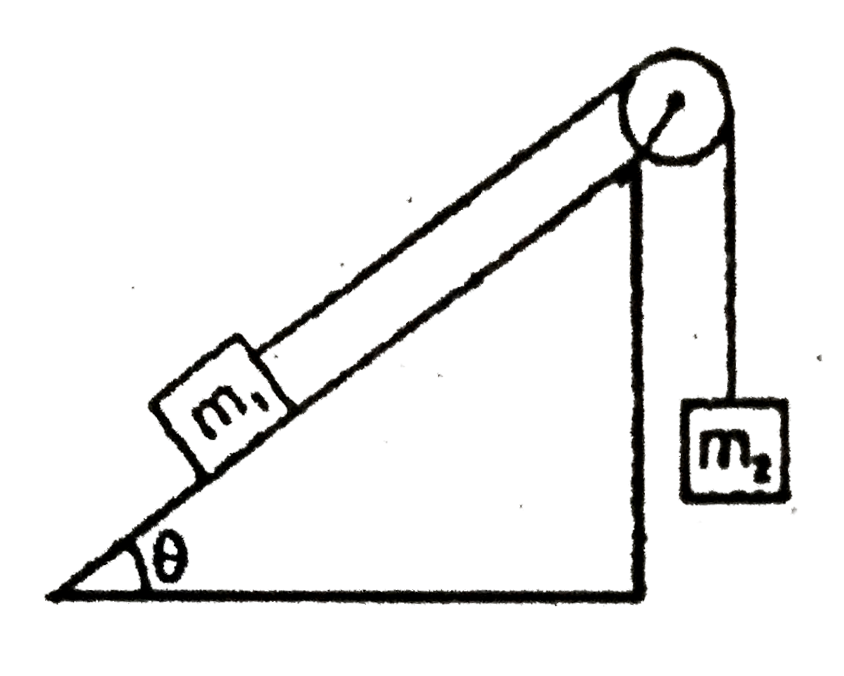
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?
View SolutionTwo blocks are kept on an inclined plane and tied to each other with a mass-less string. Coefficient of friction between m_(1) and inclined plane is mu_(1) & that betweeb m_(2) & the inclined is mu_(2) . Then :
View SolutionTwo masses M_(1) " and " M_(2) are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30^(@) and M_(1)=10 kg, M_(2)=5kg . What is the acceleration of mass M_(2) ?
View SolutionA system consists of three masses m_(1),m_(2) " and " m_(3) connected by a string passing over a pulley P. The mass m_(1) hangs freely and m_(2) " and " m_(3) are on a rough horizontal table (the coefficient of friction= mu ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m_(1) is (assume, m_(1)=m_(2)=m_(3)=m )
View SolutionA wire of 9.8×10−3kg per meter mass passes over a fricationless pulley fixed on the top of an inclined frictionless plane which makes an angle of 30∘ with the horizontal. Masses M1 & M2 are tied at the two ends of the wire. The mass M1 rests on the plane and the mass M2 hangs freely vertically downwards. the whole system is in equilibrium. Now
View SolutionTwo masses m_(1) and m_(2) ( m_(2) gt m_(1)) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
View SolutionTwo masses M_(1) and M_(2) are attached to the ends of string which passes over the pulley attached to the top of a double inclined plane. The angles of inclination of the inclined planes are alpha and beta . Take g=10ms^(-2) . If M_(1)=M_(2) and alpha=beta , what is the acceleration of the system?
View SolutionTwo weights of the mass m_(1) and m_(2) (gt m_(1)) are joined by an inextensible string of negligible mass passing over.a fixed friction-less pulley. The magnitude of the acceleration of the loads is:
View SolutionA system consists of three masses m1,m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (assume, m1=m2=m3=m)
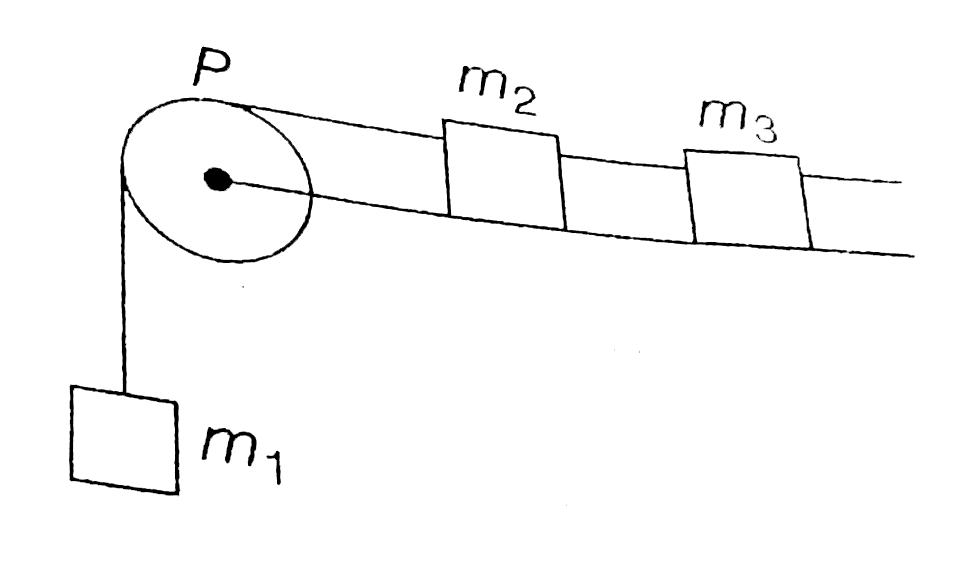
View SolutionTwo masses M_(1) " and " M_(2) are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30^(@) and M_(1)=10 kg, M_(2)=5kg . What is the acceleration of mass M_(2) ?
View SolutionA system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m1 is (Assume m1=m2=m3=m).

View Solution