A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A ) and aluminium (wire B) of equal length (shown in the figure)
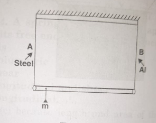
The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively.
(YAL=70×109Nm−2 and ysteel=200×109Nm−2)Solution in Punjabi
Mass m should be suspended close to wire A to have equal stresses in both the wires.
Mass m should be suspended close to B to have equal stresses in both the wires
Mass m should be suspended at the middle of the wires to have equal stresses in both the wires
Mass m should be suspended close to wire A to have equal strain in both wires.
Step by step video & image solution for A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A ) and aluminium (wire B) of equal length (shown in the figure) The cross-sectional areas of wires A and B are 1.0 mm^2 and 2.0 mm^2, respectively. (Y_(AL) = 70 xx 10^9 N m^-2 and y _(steel) = 200 xx 10^9 N m^-2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
On what factors, the modulus of elasticity depends?
View SolutionWhat is the unit of torr?
View SolutionWhat is dimension of G?
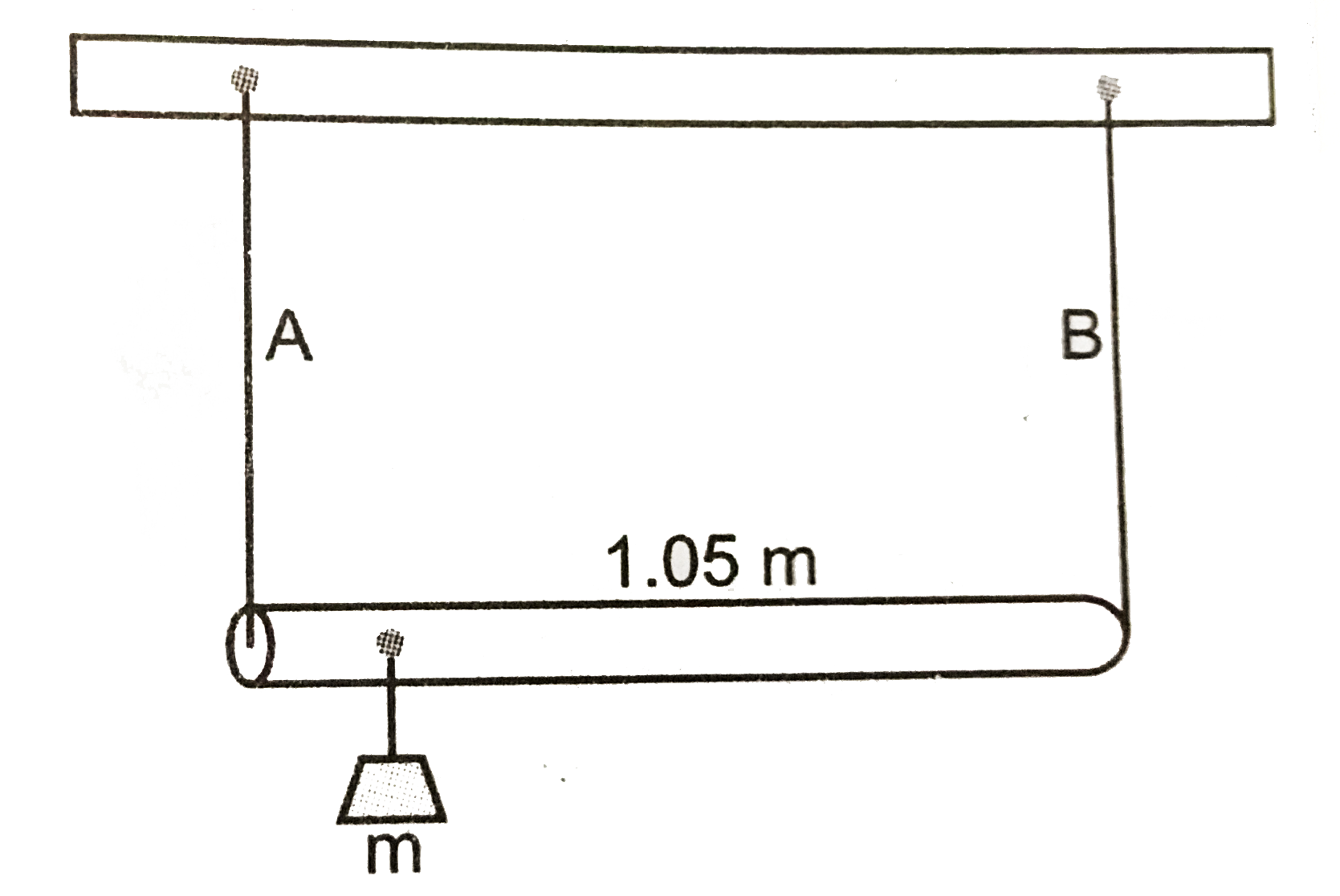
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2

View SolutionA brass of length 2 m and cross-sectional area 2.0 cm^(2) is attached end to end to a steel rod of length and cross-sectional area 1.0 cm^(2) . The compound rod is subjected to equal and oppsite pulls of magnitude 5 xx 10^(4) N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is { Y_(Brass) = 1.0 xx 10^(11) N//m^(2) and Y_(steel) = 2.0 xx 10^(11) N//m^(2)
View SolutionAn aluminium wire and a steel wire of the same length and cross section are joined end to end. The composite wire is hung from a rigid support and the load is suspended at the free end. If Y_(AL) = 7xx10^(10) N//m^(2) and Y_("steel") = 7xx10^(11) N//m^(2) , the ratio of elongation of aluminium and steel wires is
View SolutionA rod of length 1.05 m having negligible mass supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
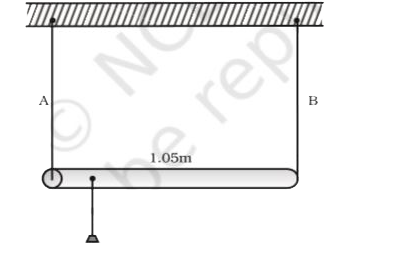
View SolutionA rod of length 1.05 m having negligible mass supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1 mm^(2) and 2 mm^(2) , respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given, Y_(steel) = 2 xx 10^(11) Nm^(-2) and Y-(alumi n i um) = 7.0 xx 10^(10)N^(-2)
View Solutionl लम्बाई तथा उपेक्षणीय द्रव्यमान की कोई छड़ अपने दो सिरों पर समान लम्बाई की दो तारों से लटकाई गई है जिनमें एक तार स्टील (तार A) का तथा दूसरा एल्यूमीनियम (तार B) का है। तार A तथा B की अनुप्रस्थ-काट के क्षेत्रफल क्रमश: 1.0 मी 2 तथा 2.0 मिमी 2 हैं
(YAI=70×109 न्यूटन/मी 2 और Ysteel=200×109 न्यूटन/मी 2)
View SolutionA rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure. The cross-sectional areas of wires A and B are 1.0 mm^(2) and 2.0 mm^(2), respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
View SolutionA rod of length 1 and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure. The cross-sectional areas of wires A and B are 1.0 mm^(2) and 2.0 mm^(2) respectively. Y_("steel”) = 200 xx 10 ^(9) Nm ^(-2) and Y_("auminium”) = 70 xx 10 ^(9) Nm ^(-2)
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2

View Solutionl लंबाई तथा उपेक्षणीय द्रव्यमान की कोई छड़ अपने दो सिरों पर समान लंबाई दो तारों से लटकाई गई है जिनमें एक तार स्टील (तार A) का तथा दूसरा एल्यूमिनियम (तार B) का है (चित्र 9.4)। तार A तथा B की अनुप्रस्थ कार के क्षेत्रफल क्रमश: 1.0mm2 तथा 2.0mm2 है।
( YAI=70×10−9Nm−2 और Ys teel=200×109Nm−2)

View SolutionA brass of length 2 m and cross-sectional area 2.0 cm^(2) is attached end to end to a steel rod of length and cross-sectional area 1.0 cm^(2) . The compound rod is subjected to equal and oppsite pulls of magnitude 5 xx 10^(4) N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is { Y_(Brass) = 1.0 xx 10^(11) N//m^(2) and Y_(steel) = 2.0 xx 10^(11) N//m^(2)
View Solution
