Show that a.(b×c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors , a, b and c.Solution in Punjabi
Step by step video solution for Show that a.(b xx c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors , a, b and c. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODYBOOK - MBDCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODYEXERCISE - EXERCISE
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - MBDCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
14 Videos
- OSCILLATIONSBOOK - MBDCHAPTER - OSCILLATIONSEXERCISE - EXERCISE
11 Videos
Similar Questions
Define centre of mass.
View SolutionIn which of the following examples of motion, can the body be considered approximately a point object:
View SolutionHow will the period of a simple pendulum change when its length is doubled?
View SolutionIf →a,→b,→care mutually perpendicular vectors of equal magnitudes, show that the vector →a+→b+→cis equally inclined to →a,→b and →c.
View SolutionFind the volume of a parallelepiped having three vectors of equal magnitude |→a| and equal inclination θ with each other.
View SolutionVolume of parallelepiped determined by vectors vec a,vec b and vec c is 5. Then the volume of the parallelepiped determined by vectors 3(vec a+vec b),(vec b+vec c) and 2(vec c+vec a) is
View SolutionShow that overset rarr(a). (overset rarr(b) xx overset rarr(c )) is equal in magnitude to the volume of the parallelopiped formed on the three vectiors, overset rarr(a), overset rarr(b) and overset rarr(c ) .
View SolutionIf a,b and c are any three vectors in space, then show that
(c+b)×(c+a)⋅(c+b+a)=[a b c]
View SolutionShow that a.(b×c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors a, b and c.
View SolutionVolume of parallelepiped formed by vectors →a×→b,→b×→c and →c×→a is 36 then find the volume of parallelepiped formed by the vectors →a,→b and →c
View SolutionShow that a.(b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors , a, b and c.
View SolutionIf →a,→b,→care mutually perpendicular vectors of equal magnitudes, show that the vector →a+→b+→cis equally inclined to →a,→band →c.
View SolutionShow that →a.(→b×→c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors, →a,→band→c
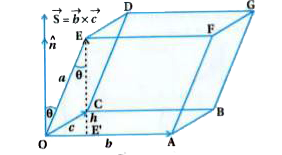
View SolutionShow that a*(bxxc) The magnitude of is equal to the volume of the six heads parallel to the three vectors a, b and c.
View SolutionIf the volume of the parallelepiped formed by three non-coplanar vectors →a,→band→c is 4 cubic units, then [→a×→b.→b×→c.→c×→a]=
View SolutionIf a,b and c are any three vectors in space, then show that
(c+b)×(c+a)⋅(c+b+a)=[a b c]
View Solution
