Question

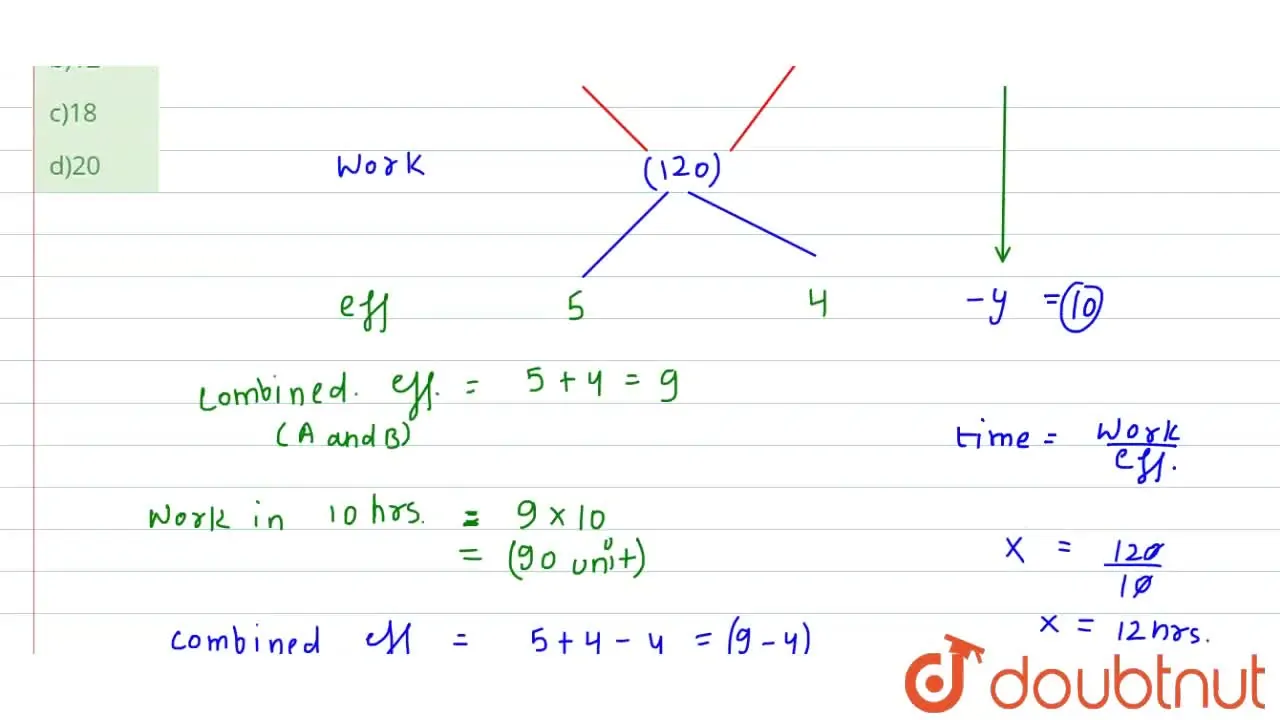
Pipes A and B can fill a tank in 24 hours and 30 hours, respectively, while pipe C can emptyl it in x hours. A and B are kept open for 10 hours at the same time and then C is opened. If the tank become empty in 90 hours, then what is the value of x? /
पाइप A और B क्रमशः 24 घंटे
और 30 घंटे में किसी टैंक को भर सकते है, जबकि पाइप C इसे x घंटे में खाली कर सकता है। A और B को एक ही समय पर 10 घंटे क लिए खुला रखा जाता है और फिर C को भी खोल दिया जाता है । यदि टैंक 90 घंटे में खाली होता है, तो x का मान कितना है?

Options

A. a)15
B. b)12
C. c)18
D. d)20

Explanation

To solve the problem step by step, we need to determine the value of x, the time taken by pipe C to empty the tank. Here’s how we can approach the problem:

Step 1: Determine the filling rates of pipes A and B
- Pipe A can fill the tank in 24 hours, so its rate of filling is:
\( \text{Rate of A} = \frac{1}{24} \text{ tank/hour} \)
- Pipe B can fill the tank in 30 hours, so its rate of filling is:
\( \text{Rate of B} = \frac{1}{30} \text{ tank/hour} \)

Step 2: Calculate the combined filling rate of A and B
- The combined rate of A and B is:
\( \text{Combined Rate} = \frac{1}{24} + \frac{1}{30} \)
- To add these fractions, we find a common denominator, which is 120:
\( \text{Combined Rate} = \frac{5}{120} + \frac{4}{120} = \frac{9}{120} = \frac{3}{40} \text{ tank/hour} \)

Step 3: Calculate the amount of water filled by A and B in 10 hours
- In 10 hours, the amount of tank filled by A and B is:
\( \text{Work done by A and B in 10 hours} = \text{Combined Rate} \times \text{Time} = \frac{3}{40} \times 10 = \frac{30}{40} = \frac{3}{4} \text{ of the tank} \)

Step 4: Determine the remaining amount of the tank to be emptied
- After A and B have worked for 10 hours, the remaining amount of the tank is:
\( \text{Remaining} = 1 - \frac{3}{4} = \frac{1}{4} \text{ of the tank} \)

Step 5: Set up the equation for pipe C
- Let the rate of pipe C be \( \frac{1}{x} \) tank/hour (since it empties the tank in x hours).
- When C is opened, the combined rate of A, B, and C is:
\( \text{Combined Rate of A, B, and C} = \frac{3}{40} - \frac{1}{x} \)
- The time taken to empty the remaining \(\frac{1}{4}\) of the tank is given as 90 hours. Thus, we can set up the equation:
\( \left(\frac{3}{40} - \frac{1}{x}\right) \times 90 = -\frac{1}{4} \)

Step 6: Solve the equation
- Rearranging the equation gives:
\( \frac{3}{40} - \frac{1}{x} = -\frac{1}{360} \)
- Now, multiply through by \( 40x \) to eliminate the fractions:
\( 3x - 40 = -\frac{40}{360}x \)
- Simplifying the equation:
\( 3x + \frac{1}{9}x = 40 \)
- Converting \(\frac{1}{9}\) to a fraction with a common denominator:
\( \frac{27}{9}x + \frac{1}{9}x = 40 \implies \frac{28}{9}x = 40 \)
- Thus,
\( x = \frac{40 \times 9}{28} = \frac{360}{28} = 12.857 \text{ hours} \)

Step 7: Final Calculation
- Since we need the time in whole hours, we can round \( x \) to the nearest whole number, which is approximately 13 hours.

Conclusion
The value of \( x \) is approximately 13 hours.