Corner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).Solution in Odia
The correct Answer is:2p=q
Step by step video, text & image solution for Corner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0. Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VERY SIMILAR TEST 8Book:ARIHANT PRAKASHANChapter:VERY SIMILAR TEST 8Exercise:Section C
Explore 25 Videos
- VERY SIMILAR TEST 8Book:ARIHANT PRAKASHANChapter:VERY SIMILAR TEST 8Exercise:Section C
Explore 25 Videos
- VERY SIMILAR TEST 7Book:ARIHANT PRAKASHANChapter:VERY SIMILAR TEST 7Exercise:Section C (30 MARKS)
Explore 32 Videos
- VERY SIMILAR TEST 9Book:ARIHANT PRAKASHANChapter:VERY SIMILAR TEST 9Exercise:Section C
Explore 24 Videos
Similar Questions
If y=[x+√x2+a2]n, then prove that dydx=ny√x2+a2
View SolutionIf y=[x+√x2+a2]n, then prove that dydx=ny√x2+a2
View SolutionIf cos y = x cos(a+y) then prove that
dydx=cos2(a+y)sina
View SolutionIf ex+ey=ex+y, then prove that
dydx=ex(ey−1)ey(ex−1) or dydx+ey−x=0.
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1), and (3,0). Let Z=px+qy. Where p,q<0 Condition on p and q, so that the minimum of Z occurs at (3,0) and (1,1) is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3),(1,1)and(3,0). Let z=px+qy, where p,q>0. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
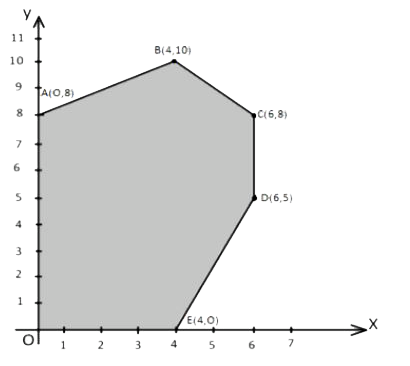
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.
View SolutionCorner poins of the feasible region determned by the system of linear constrainsts are (0,3), (1,1), and (3,0). Let Z=px+qy. Where p,q<0 Condition on p and q, so that the minimum of Z occurs at (3,0) and (1,1) is
View SolutionThe vertices of the feasible region determined by some linear constraints are (0,2),(1,1),(3,3),(1,5). Let Z=px+qy where p,q>0. The condition on pandq so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is .......
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q, so that the maximum of Z occurs at (3, 0) and (1, 1) is ……….
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system linear constraints are (0,10), (5,5), (15,15), (0,20). Let Z = px+ qy, where p, q>0, condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).
View Solution

