The vertices of the feasible region determined by some linear constraints are . Let where . The condition on so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ....... Solution in Gujrati
The correct Answer is:A
Step by step video, text & image solution for The vertices of the feasible region determined by some linear constraints are (0,2), (1,1),(3,3), (1,5). Let Z=px + qy where p,q gt 0. The condition on p and q so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ....... by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BOARD'S QUESTION PAPER MARCH - 2020BOOK - KUMAR PRAKASHANCHAPTER - BOARD'S QUESTION PAPER MARCH - 2020EXERCISE - PART - B (Section - A)
4 Videos
- BOARD'S QUESTION PAPER MARCH - 2020BOOK - KUMAR PRAKASHANCHAPTER - BOARD'S QUESTION PAPER MARCH - 2020EXERCISE - PART - B (Section - B)
7 Videos
- APPLICATION OF INTEGRALSBOOK - KUMAR PRAKASHANCHAPTER - APPLICATION OF INTEGRALSEXERCISE - PRACTICE PAPER ( SECTION -D)
2 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - KUMAR PRAKASHANCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Practice Paper - 5 (Section-D)
4 Videos
Similar Questions
Find the values of each of the following :
tan12[sin−12x1+x2+cos−11−y21+y2],|x|<1,y>0andxy<1
View SolutionConsider f,R+→[−5,∞) given by f(x)=9x2+6x−5. Show that f is invertible with f−1(y)=⎛⎜ ⎜⎝(√y+6)−13⎞⎟ ⎟⎠, where R+ is the set of all non-negative real numbers.
View SolutionFind the area of the regaion enclosed by {(x,y):y2≤4x,4x2+4y2≤9}.
View SolutionIf y=ecos−1x,−1≤x≤1, then prove that (1−x2)d2ydx2−xdydx−y=0
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3),(1,1)and(3,0). Let z=px+qy, where p,q>0. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
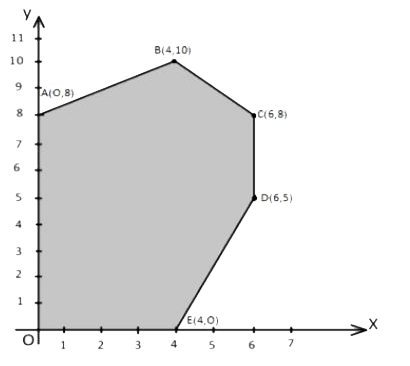
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q, so that the maximum of Z occurs at (3, 0) and (1, 1) is ……….
View SolutionThe corner points of the feasible region determined by some inequality are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p,q>0 condition on p and q so that the maximum of Z occurs at both (15, 15) and (0, 20) is …………
View SolutionThe vertices of the feasible region determined by some linear constraints are (0, 2), (1, 1), (3, 3), (1, 5). Let Z = px + qy where p, q gt 0. The condition on p and q so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ……..
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system linear constraints are (0,10), (5,5), (15,15), (0,20). Let Z = px+ qy, where p, q>0, condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).
View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).
View Solution
