ABC is an isosceles triangle with AB = AC and D is the mid-point of base BC.
(a) State three pairs of equal parts in the triangles ABD and ACD.
(b) Is ΔABD≅ΔACD. If so why?
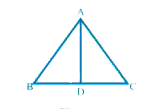
Step by step video & image solution for ABC is an isosceles triangle with AB = AC and D is the mid-point of base BC. (a) State three pairs of equal parts in the triangles ABD and ACD. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
ABC is an isosceles triangle such that AB=ACand ADis the median to the base BCwith ∠ABC=35∘ . Then ∠BAD is
A35∘B55∘C70∘D110∘ - Question 2 - Select One
ABC is an isosceles triangle such that AB = AC and ∠B=35∘. AD is the medium to the base BC. Then ∠BAD is:
A55∘B70∘C35∘D110∘
In Fig.19,Δ ABC is isosceles with AB=AC, D is the mid-point of base BC. IsΔADB≅ΔADC? State the three pairs of matching parts you use to arrive at your answer.
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionABC is an isosceles triangle with AB=AC and D is a point on ABC BC such that AD⊥BC (see figure ). To prove that ∠BAD=∠CAD a student proceeded as follows
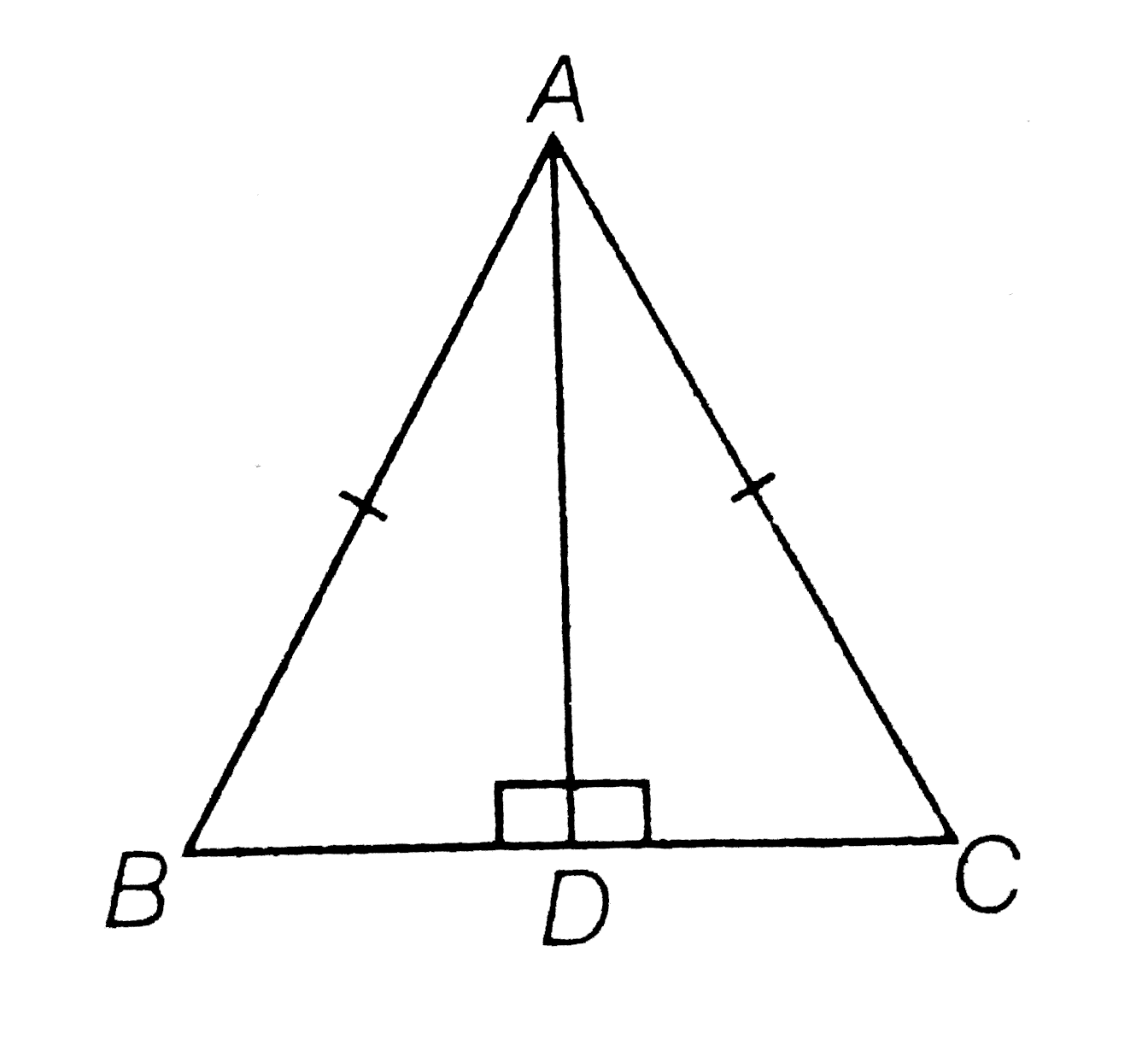
InΔABDandΔACD,we have
AB=AC [ Given]
∠B=∠C [∵ AB=AC ]
and ∠ADB=∠ADC
Therefore ΔABD≅ΔACD [by AAS congruence rule]
So , ∠BAD=∠CAD [byCPCT]
What is the defect in the above argument ?View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
 View Solution
View SolutionLet ABC be an isosceles triangle with AB=AC and let D,E,F be the mid-points of BC,CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
"
View Solution
