A potential difference applied to the ends of a wire made up of an alloy drives a current through it such that ,where r is the distance of the point from the axis. If R be the radius of the wire, then find the total current through any cross section of the wire.
To find the total current through any cross-section of the wire, we start with the given current density J as a function of the distance r from the axis of the wire:
J=α+βr
where α and β are constants, and R is the radius of the wire.
Step 1: Define the differential current dI
The current density J is defined as the current per unit area. Therefore, the differential current dI through a thin annular ring of radius r and thickness dr can be expressed as:
dI=J⋅dA
where dA is the area of the annular ring.
Step 2: Calculate the area dA
The area dA of the annular ring can be calculated as the circumference of the ring multiplied by its thickness:
dA=2πrdr
Step 3: Substitute dA into dI
Now, substituting dA into the expression for dI:
dI=J⋅dA=(α+βr)(2πrdr)
Step 4: Expand dI
Expanding the expression for dI:
dI=2πr(α+βr)dr=2π(αr+βr2)dr
Step 5: Integrate to find total current I
To find the total current I through the cross-section of the wire, we need to integrate dI from r=0 to r=R:
I=∫R0dI=∫R02π(αr+βr2)dr
Step 6: Perform the integration
We can split the integral:
I=2π(∫R0αrdr+∫R0βr2dr)
Calculating each integral separately:
1. For the first integral:
∫R0αrdr=α(r22)R0=αR22
2. For the second integral:
∫R0βr2dr=β(r33)R0=βR33
Step 7: Combine results
Substituting back into the expression for I:
I=2π(αR22+βR33)
This simplifies to:
I=π(αR2+23βR3)
Final Result
Thus, the total current through any cross-section of the wire is given by:
I=π(αR2+23βR3)
---
Similar Questions
A potential difference of 100 V is applied across a wire for two minutes. If the current through the wire is 0.1 A , find the heat produced in houle .
View SolutionThe current through a wire depends on time as i=(2+3t)A. Calculate the charge crossed through a cross section of the wire in 10sec.
View Solution
Knowledge Check
As is the cross sectional area and ρ is the specific resistance of a potentiometer wire. If I is the current passing through the potentiometer wire, then the potential gradient along the length of the wire is given by
AIAρBIAρCIρADIρA
Calculate the electric current through a wire if 10 coulombs of charge flow through a cross section of the wire in 2 seconds.
View SolutionA potential difference of 100 V is applied across a wire for 6 minutes and 58 seconds. If the current through the wire is 0.1 A, find the heat produced in calorie.
View SolutionA potential difference is applied across a wire of length 1 m and resistance 10Ω , such that the current through it is 1 A. The electric field inside the wire is __________N/C.
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View Solution5.A current through a wire depends on time as i = α 0 t + β t where alpha_(0)=20A/s and beta=8As^(-2).Find the charge crossed through a " section of the wire in 15s
View SolutionSuppose that the current density in a wife of radius a varies with r according to J=Kr2, where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r < a and (b) r > a

View SolutionFind the potential difference the points a and b of the circuit(figure). If a and b are joined by a wire what is the current through the 12-V cell?
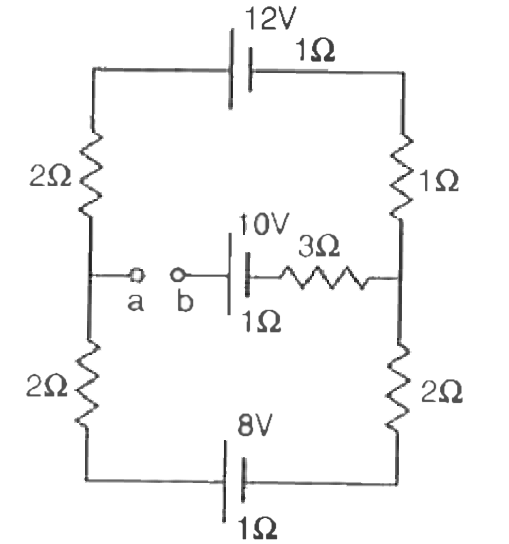
View Solution