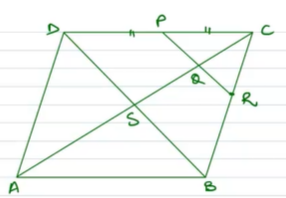
P,Q and R are, respectively, the mid-points of sides BC,CA and AB of a triangle ABC , PR and BQ meet at X.CR and PQ meet at Y . Prove that XY=14BC.
XY=13BC
XY=23BC
XY=14BC
XY=25BC
Step by step video solution for P ,Q and R are, respectively, the mid-points of sides B C ,C A and A B of a triangle A B C , P R and B Q meet at XdotC R and P Q meet at Y . Prove that X Y=1/4B Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
P, Q and R are, respectively, the mid points of sides BC, CA and AB of a triangle ABC and AD is the perpendicular from vertex A to BC,then prove that the points P,Q,R and D are cyclic.
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionIn ABC and PQR Figure, AB=PQ,BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX =∠PQY. Prove that ABC≅PQR. Figure
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
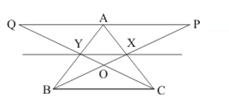
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View Solution
