$C_{1}$ and $C_{2}$ are two concentric circles, the radius of $C_{2}$ being twice that of $C_{1}$ . From a point P on $C_{2}$ , tangents PA and PB are drawn to $C_{1}$ . Prove that the centroid of triangle PAB lies on $C_{1}$ .Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Let the coordinates of point P be $(2 r cos θ, 2 r sin θ)$
We have , OA = r, OP = 2r
Since, $Δ O A P$ is a right angled triangle.

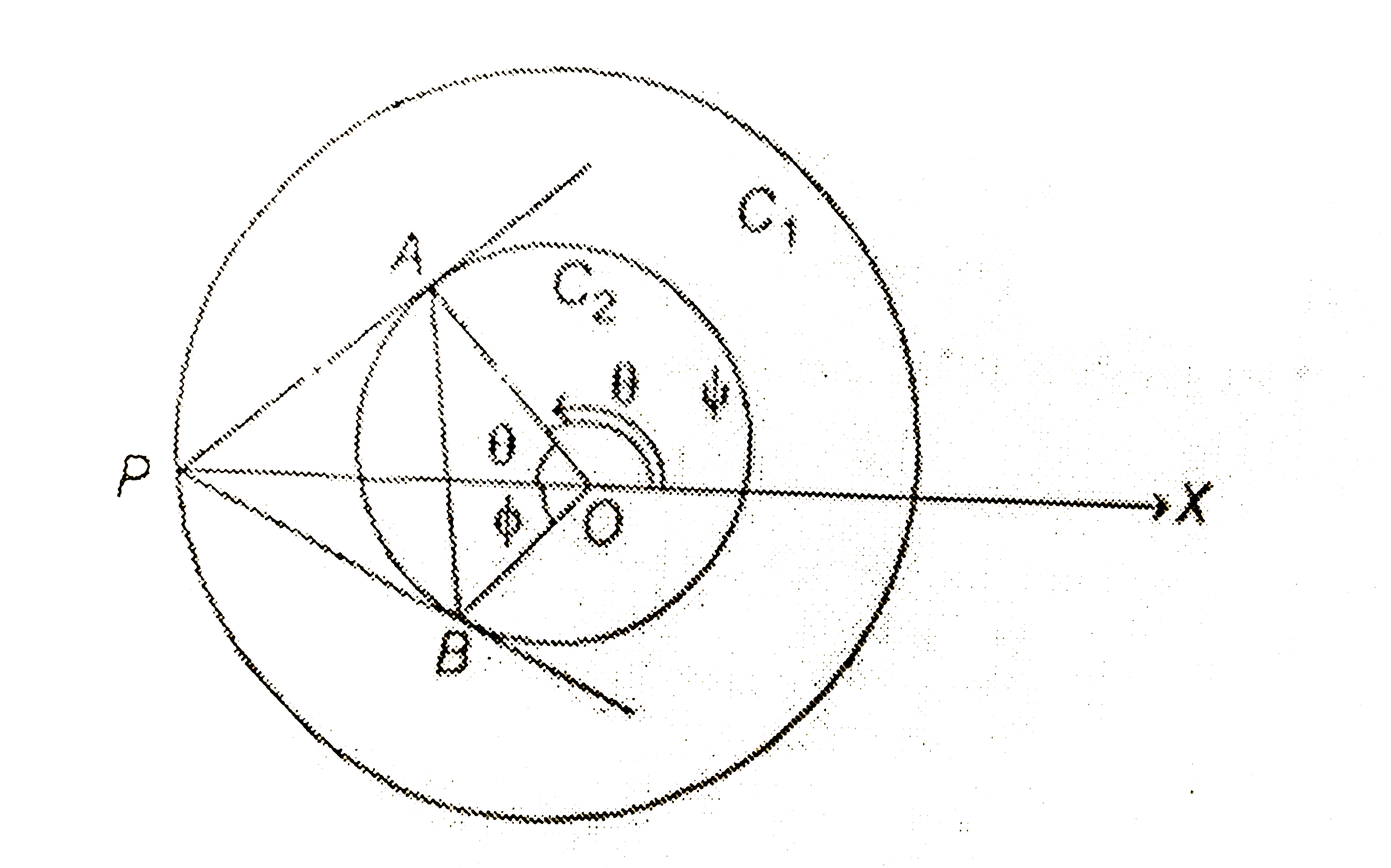
$cos ϕ = 1 / 2 \Rightarrow ϕ = π / 3$
$∴$ Coordinates of A are ${cos (θ - π / 3), r sin (θ - π / 3)}$
If p, q is the centroid of Delta PAB, then
$p = \frac{1}{3} [r cos (θ - π / 3) + r cos (θ + π / 3) + 2 r cos θ]$
$= \frac{1}{3} [r (2 cos \frac{θ - \frac{π}{3} + θ + \frac{π}{3}}{2} \cdot cos \frac{θ - \frac{π}{3} - θ - \frac{π}{3}}{2}) + 2 r cos θ]$
$\frac{1}{3} [r {2 cos θ π / 3} + 2 r cos θ]$
$= \frac{1}{3} [r \cdot cos θ + 2 r cos θ] = r cos θ$
and $q = \frac{1}{3} [r sin (θ - \frac{π}{3}) + r sin (θ + \frac{π}{3}) + 2 r sin θ]$
$= \frac{1}{3} [r (2 sin \frac{θ - \frac{π}{3} + θ + \frac{π}{3}}{2} \cdot cos \frac{θ - \frac{π}{3} - θ - \frac{π}{3}}{2}) + 2 r sin θ]$
$= \frac{1}{3} [r sin (2 sin θ cos π / 3) + 2 r sin θ]$
$= \frac{1}{3} [r (sin θ) + 2 r sin θ] = r sin θ$
Now, (p, q) = $(r cos θ, r sin θ) lies on x^{2} + y^{2} = r^{2}$ which is called $C_{1}$ .

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile