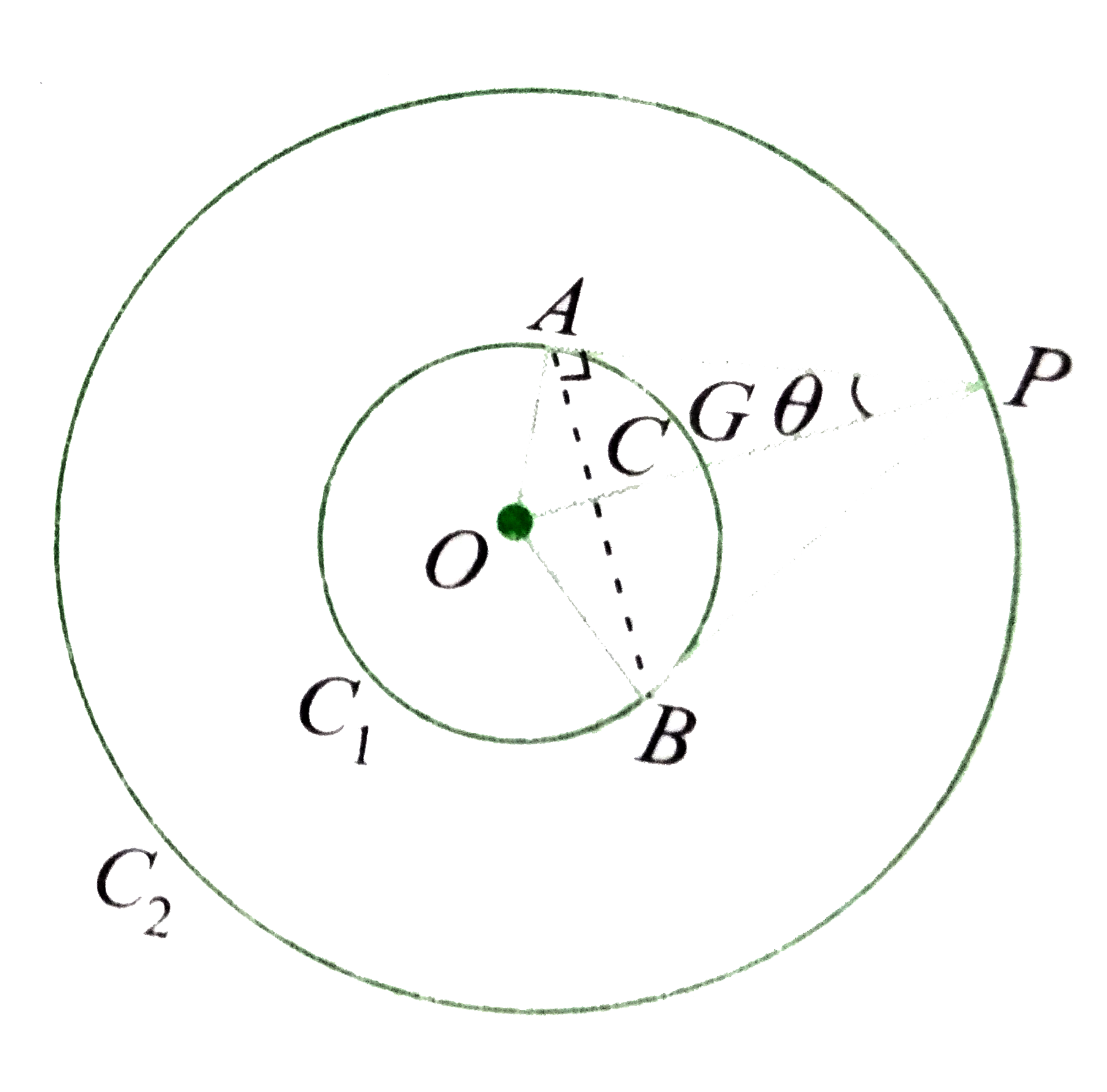
C1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1
Let r be the radius of C1 and 2r be the radius of C2.Then, OA=OB=r
and OP=2r
Since PA and PB are tangents to C1,
∠OAP=∠OBP=90∘
Let OP meets C1 at G.
Let ∠OPA=θ. Then,
sinθ=OAOP=r2r=12
or θ=30∘
or ∠AOP=60∘
In ΔOAC,
cos60∘=OCOA
or 12=OCror OC=r2
∴PC=2r−r2−3r2
Also, CG=r−OC=r−r2=r2
Clearly, CG=13PC
Therefore, G is the centroid of ΔABP.
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Examples
Explore 13 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.1
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
C1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Then the centroid of the triangle PAB (a) lies on C1 (b) lies outside C1 (c) lies inside C1 (d) may lie inside or outside C1 but never on C1
View SolutionC1andC2, are the two concentric circles withradii r1andr2,(r1<r2). If the tangents drawnfrom any point of C2, to C1, meet again C2, at theends of its diameter, then
View SolutionFrom a point P outside a circle with centre at C, tangents PA and PB are drawn such that 1(CA)2+1(PA)2=116, then the length of chord AB is
View SolutionThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
View SolutionThe centres of two circles C1andC2 each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C1andC2 and C be a circle touching circles C1andC2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C, is
View SolutionA circle C1 has radius 2 units and a circles C2 has radius 3 units. The distance between the centres of C1 and C2 is 7 units. If two points, one tangent to both circles and the other passing through the centre of both circles, intersect at point P which lies between the centers of C1andC2, then the distance between P and the centre of C1 is
View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
View SolutionThere are two circles C1 and C2 touching each other and the coordinate axes, if C1 is smaller than C2 and its radius is 2 units, then radius of C2, is
View SolutionA (c,0) and B (-c,0) are two points . If P is a point such that PA + PB = 2a where 0<c<a, then find the locus of P.
View SolutionIf a, b, c are in G.P. and also a, b, c are in A.P.
Prove that: 1a+1c=2b
View Solution