Sixteen players S1,S2,…,S16 play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players decided to the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.
(a) Find the prabability that the player S1 is among the eight winners.
(b) Find the probability that exactly one of the two players S1andS2 is among the eight winners. Solution in Tamil
The correct Answer is:A, B
(i) Probability of S1to be among the eight winners
=(Probability ofS1being a pair)
× (Prbability f S1 winnig the group)
=1×12=12 [since S1 is definitely in a group]
(ii)If S1andS2 are in two separately, then exactly one wins.
IF S1andS2 will be among the eight winners. IF S1 wins and S2 loses or S1 losses and S2 wins.
Now, the prbability of S1.S2 being the same pair and one wins
=(Probability of S1,S2 " being in the same pair" )<br>xx(Probabilityofanyo≠w∈n∈g∈thepair).<br>andtheprobabilityofS_(1),S_(2)be∈gthesamepair<br>=(n(E))/(n(S))<br>where,n(E)=theνmberofways∈which16personscanbe÷d∈8pairs.<br>therefore n(E)=((14)!)/((2!)^(7)*7!)and n(S)=((16)!)/((2!)^(8)*8!)<br>thereforeProbabilityofS_(1) and S_(2)be∈g∈thesamepair<br>=((14)!*(2!)^(8)*8!)/((2!)^(7)*7!*(16)!)=(1)/(15)<br>Theprobabilityofanyo≠w∈∈g∈thepairsofS_(1),S_(2)=P(certa∈event)=1<br>thereforeThepairsofS_(1),S_(2)be∈g∈twopairsseparatelyandS_(1)w∈s,S_(2)losses+TheprobabilityofS_(1),S_(2)be∈g∈twopairsseparatelyandS_(1)loses,S_(2)w∈s.<br>=[1-((((14)!)/((2!)^(7)*7!))/(((16)!)))/((2!)^(8)*8!)]xx(1)/(2)xx(1)/(2)+[1-((((14)!)/((2!)^(7)*7!))/(((16)!)))/((2!)^(8)*8!)]xx(1)/
(2)xx(1)/(2)<br>=(1)/(2)xx(14xx(14)!)/(15xx(14)!)=(7)/(15)<br>thereforeRequiredprobability=(1)/(15)+(7)/(15)=(8)/(15)
Similar Questions
Eight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
05:46View SolutionSixteen players S1, S2, S3,…,S16 play in a tournament. Number of ways in which they can be grouped into eight pairs so that S1 and S2 are in different groups, is equal to
03:41View Solutionसोलह खिलाड़ी s1,s2,………………,s16 एक टूर्नामेंट खेलते हैं उन्हें यादृच्छया 8 युग्मों में विभाजित किया जाता है । युग्म के दो खिलाड़ियों के मध्य खेल के आधार पर प्रत्येक युग्म में एक विजेता निर्धारित किया जाता है (माना जाए कि सभी खिलाड़ी समान क्षमता के हैं) आठ विजेताओं में से दो खिलाड़ी s1 तथा s2 में से केवल एक के होने की प्रायिकता है
04:18View SolutionIn a badminton tournament each player played one game with all the other players. How many players participated in the touinament if they played 105 games in all?
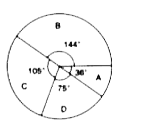
02:18View SolutionThe adjoining diagram shows a pie-chart with central angles for number of players playing four games A, B, C and D. If each player takes part in only one game and there are 480 players in all, find :
(i) how many players play the game D?
(ii) how many players do not play game B?
(iii) what is the ratio of players playing game A to the players playing game C ?
(iv) what percentage of players are playing game B?
 03:51View Solution
03:51View SolutionIn a badminton each player played one game with ll the other players. Number of players participated in the tournament if they played 105 games is
03:34View SolutionSixteen players S_1,S_2, ..., S_(16) play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.Find the probability that the player S_1 is among the eight winners.
03:30View SolutionEight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
15:32View Solution
