If →a,→b,→c and →d are the unit vectors such that
(→a×→b).(→c×→d)=1 and →a,→c=.12, then Solution in Tamil
→a,→b,→c are non -coplanar
→a,→b,→d are non- coplanar
→b,→d are non-parallel
→a,→d are parallel and →b,→c are parallel
The correct Answer is:C
Let angle between →a and →bbe01,→cand vec( d) be 0_(2) and→a×→b and →b×→d be 0 .
Since (→a×→b).(→c×→d)=1
⇒sin01. sin 02. cos0=1
⇒01=90∘,02=90∘,0=0∘
⇒→a⊥→b,→c⊥→d,(→d×→d)∣∣(→c×→d)
S⊙,→a×→b=k(→c×→d) and →a×→b=k(→c×→d)
⇒(→a×→b). →c=k(→c×→d).(→c
and (→a×→b). →d=k(→c×→d).→d ltbgt ⇒(→a,→b,→c and →a,→b,→d are coplanar vectors so options (a) and (b) are incorrect.
Let →b∣∣→d⇒→b=±→d
As (→a×→b).(→c×→d)=1⇒(→a×→b).(→c×→b)=±1
⇒[→a×→b→c→b]=±1⇒[→c→b→a×→b]=±1
⇒→a. vec(a) =+-1 [:' vec(a) .→b=0]
Which is a contradiction so
option (c ) is correct.
Let option (d) is correct.
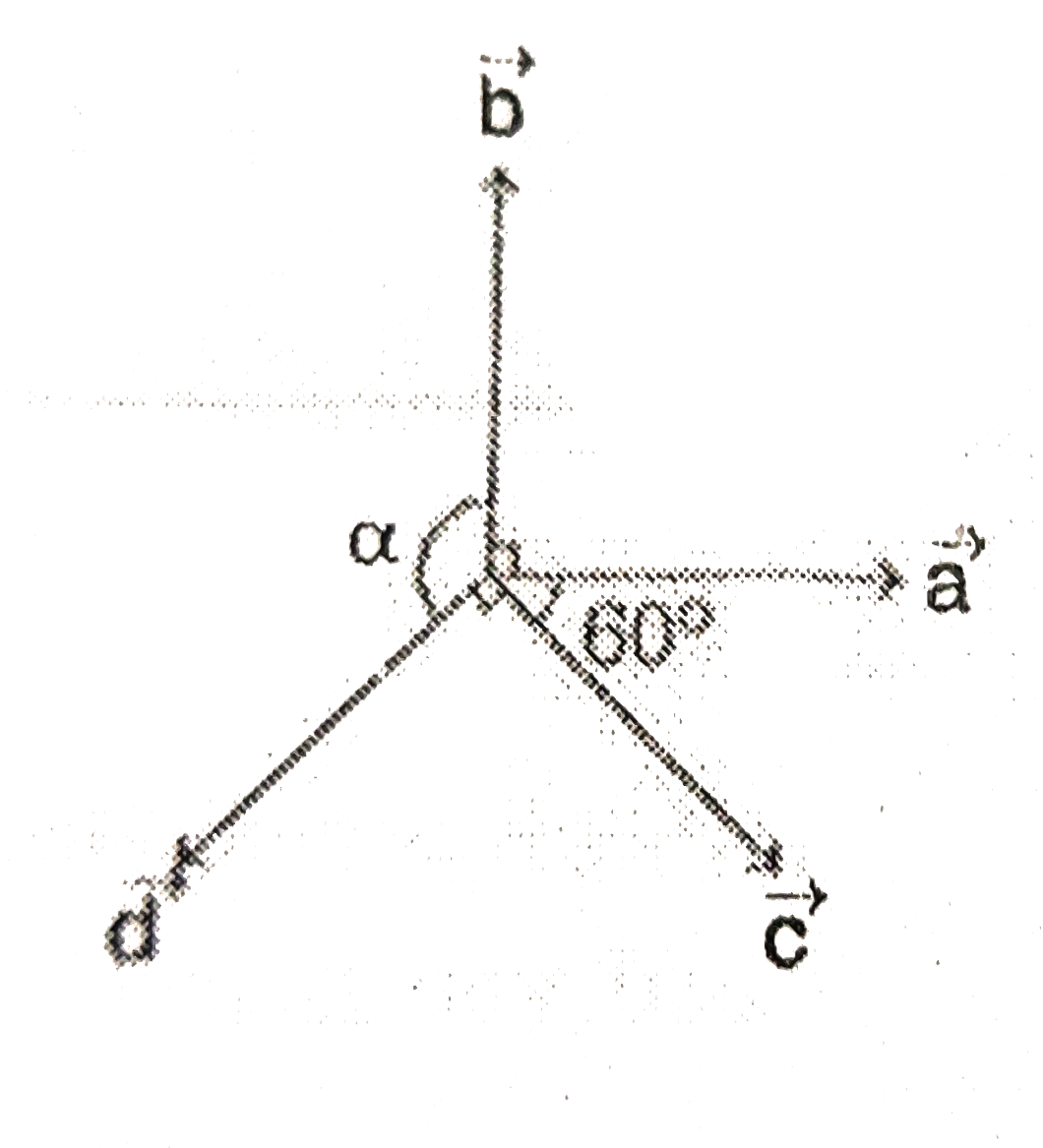
⇒→d=±→a
and →c=±→b
As (→a×→d).(→c×→d)=1
⇒(→a×→d).(→b×→a)=±1
Which is a contradiction so option (d) is incorrect,
Alternatively , options (c ) and (d) may be observed from the given figure .
Similar Questions
If →a,→b,→c are non-coplanar unit vectors such that
→a×(→b×→c)=(→b+→c)√2, then the angle between →a and →b is
View SolutionIf →A,→B and →c are vectors such that ∣∣→B∣∣=∣∣→C∣∣ . Prove that ∣∣(→A+→B)×(→A+→C)∣∣×(→B×→C).(→B+→C)=→0
View SolutionIf the vectors →b,→c,→d are not coplanar then prove than the vectors (→a×→b)×(→c×→d)+(→a×→c)×(→d×→b)
+(→a×→d)×(→b×→c) is parallel to →a
View SolutionIf [−a×−b×−c−c×−a]=λ[−a−b−c], then λ=
View Solution(−a+2−b−−c)(−a−−b)×(−a−−b−−c) is equal to
View SolutionIf four points A(−a),B(−b),C(−c)&D(−d) are coplanar then show that [−a−b−d]+[−b−c−d]+[−c−a−d]=[−a−b−c]
View SolutionIf overset(to)(a),overset(to)(b),overset(to)(c ),overset(to)(d) are four distinct vectors satisfying the conditions overset(to)(a)xxoverset(to)(b)=overset(to)(c )xx overset(to)(d) " and " overset(to)(a)xxoverset(to)(c ) = overset(to)(b)xx overset(to)(d) then prove that , overset(to)(a).overset(to)(b)+overset(to)(c ). overset(to)(d) ne overset(to)(a). overset(to)(c)+overset(to)(b).overset(to)(d) .
View Solution