If →a,→b,→c and →d are the unit vectors such that
(→a×→b).(→c×→d)=1 and →a,→c=.12, then
A
→a,→b,→c are non -coplanar
B
→a,→b,→d are non- coplanar
C
→b,→d are non-parallel
D
→a,→d are parallel and →b,→c are parallel
Video Solution
Text Solution
The correct Answer is:C
Let angle between →a and →bbe01,→cand vec( d) be 0_(2) and→a×→b and →b×→d be 0 .
Since (→a×→b).(→c×→d)=1
⇒sin01. sin 02. cos0=1
⇒01=90∘,02=90∘,0=0∘
⇒→a⊥→b,→c⊥→d,(→d×→d)∣∣(→c×→d)
S⊙,→a×→b=k(→c×→d) and →a×→b=k(→c×→d)
⇒(→a×→b). →c=k(→c×→d).(→c
and (→a×→b). →d=k(→c×→d).→d ltbgt ⇒(→a,→b,→c and →a,→b,→d are coplanar vectors so options (a) and (b) are incorrect.
Let →b∣∣→d⇒→b=±→d
As (→a×→b).(→c×→d)=1⇒(→a×→b).(→c×→b)=±1
⇒[→a×→b→c→b]=±1⇒[→c→b→a×→b]=±1
⇒→a. vec(a) =+-1 [:' vec(a) .→b=0]
Which is a contradiction so
option (c ) is correct.
Let option (d) is correct.
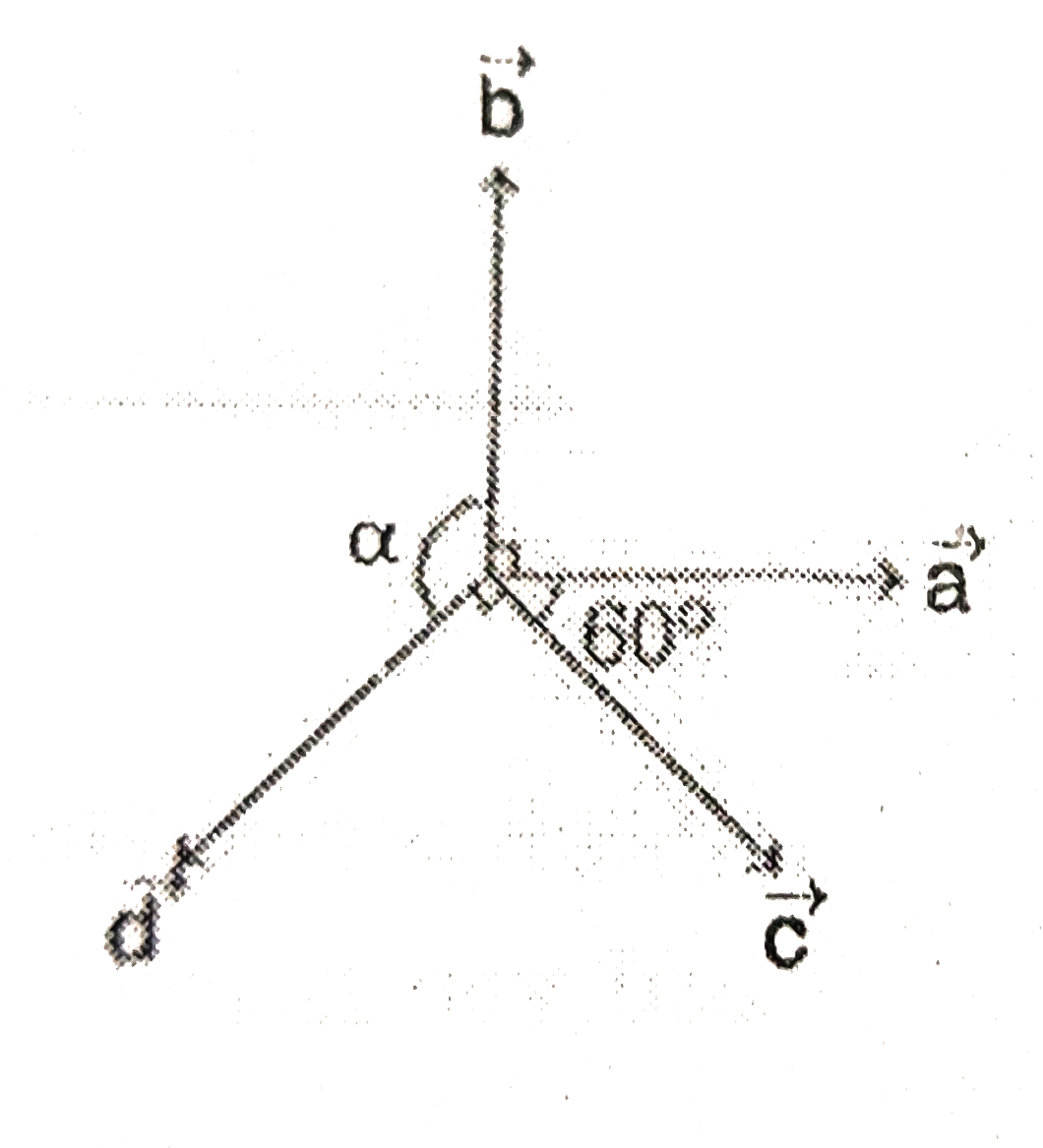
⇒→d=±→a
and →c=±→b
As (→a×→d).(→c×→d)=1
⇒(→a×→d).(→b×→a)=±1
Which is a contradiction so option (d) is incorrect,
Alternatively , options (c ) and (d) may be observed from the given figure .
|
Similar Questions
Knowledge Check
If →a,→b and →c are three non- coplanar vectors then
(→a+→b+→c).[(→a+→b)×(→a+→c)] equalsA0B[→c→b→c]C[→c→b→c]D[→a→b→c]If →a,→b and →c are unit coplanar vectors then the scalar triple product [2→a−→b2→b−→c2→c−→a] is
A0B1C−√3D√3Let the vectors →a,→b,→c and →d be such that
(→a×→b)×(→c×→d)=→0. If P1 and P2 are planes determined by the pairs of vectors →a,→b and oerset(→)(c),→d respectively then the angle between P1 and P2 isA0Bπ/4Cπ/3Dπ/2
A,B,C and d are four points in a plane with position vectors →a,→b,→c and →d respectively such that (→a−→d).(→b−→c)=(→b−→d)(→c−→a)=0 The point D then is the .... of the ΔABC
View SolutionThe scalar →A.[(→B×→C)×(→A+→B+→C)] equals
View Solutionif →a,→b and →c are unit vectors then
∣∣→a−→b∣∣2+∣∣→b−→c∣∣2+|→c−→a|2 does not exceed
View SolutionLet →a,→b,→c be unit vectors such that →a+→b+→c=→0.
Which one of the following is correct ?
View SolutionIf →a,→b,→c are non-coplanar unit vectors such that
→a×(→b×→c)=(→b+→c)√2, then the angle between →a and →b is
View Solution