Suppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is Solution in Tamil
|→a|
|→u|+|→u.→a|
|→u|+|→u.→a|
|→u|+∣→u.(→a+→b)
The correct Answer is:A, C
Let 0 be the angle between →a and →b . Since →a and →b are non- collinear vectors then 0 ≠ 0 and 0≠π.
we have →a. →b=|→a|→a∣∣ cos 0
= cos 0 [∵|→a|=1,∣∣→b∣∣=1 given ]
Now →u=→a−(→a. →b)→b⇒|→u|=∣∣→a. →b∣∣
⇒|→u|2=|→a|2−(→a. →b)→b∣∣2
⇒|→u|2=1+cos20⇒|→u|2−sin20
Also →v=→a×→b
⇒|→v|2=∣∣→a×→b∣∣2⇒|→v|2=|a|2|b|2sin20
⇒|→v|2=sin20∴|→u|2=|→v|2
Now , →u.→a=[→a−(→a.→b)→b].→a=→a.→a−(→a.→b)(→b.→a)
=(→a)2−cos20=1−cos20=sin20
∴|→u|+|→u.→a|=sin20≠|→v|
→u.→b=[→a−(→a. →b)→b].→b
=→a.→b−(→a. →b)(→b. →b)=→a. →b−→a. →b∣∣→b∣∣2
=→a. →b−→a. →b=0
Also →u. (→a+→b)=∣→u. →a+→u. →b=→u. →a
⇒|→u|+∣∣→u. (→a+→b)=∣∣→u|+→u. →a≠|→v∣∣
Similar Questions
If →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1 . If →P+→Q−→S=0 angle between →P and →S is θ2 . The ratio of θ1 to θ2 is
View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
View SolutionIf →P+→Q=→Rand P=Q=R√2, then find the angles between the pairs of vectors (→P+→Q),(→Q,→R)and(→R,→P)respectively
View SolutionSuppose that vec p,vecqand vecr are three non- coplaner in R^(3) ,Let the components of a vector vecs along vecp , vec q and vecr be 4,3, and 5, respectively , if the components this vector vec s along (-vecp+vec q +vecr),(vecp-vecq+vecr) and (-vecp-vecq+vecr) are x, y and z , respectively , then the value of 2x+y+z is
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
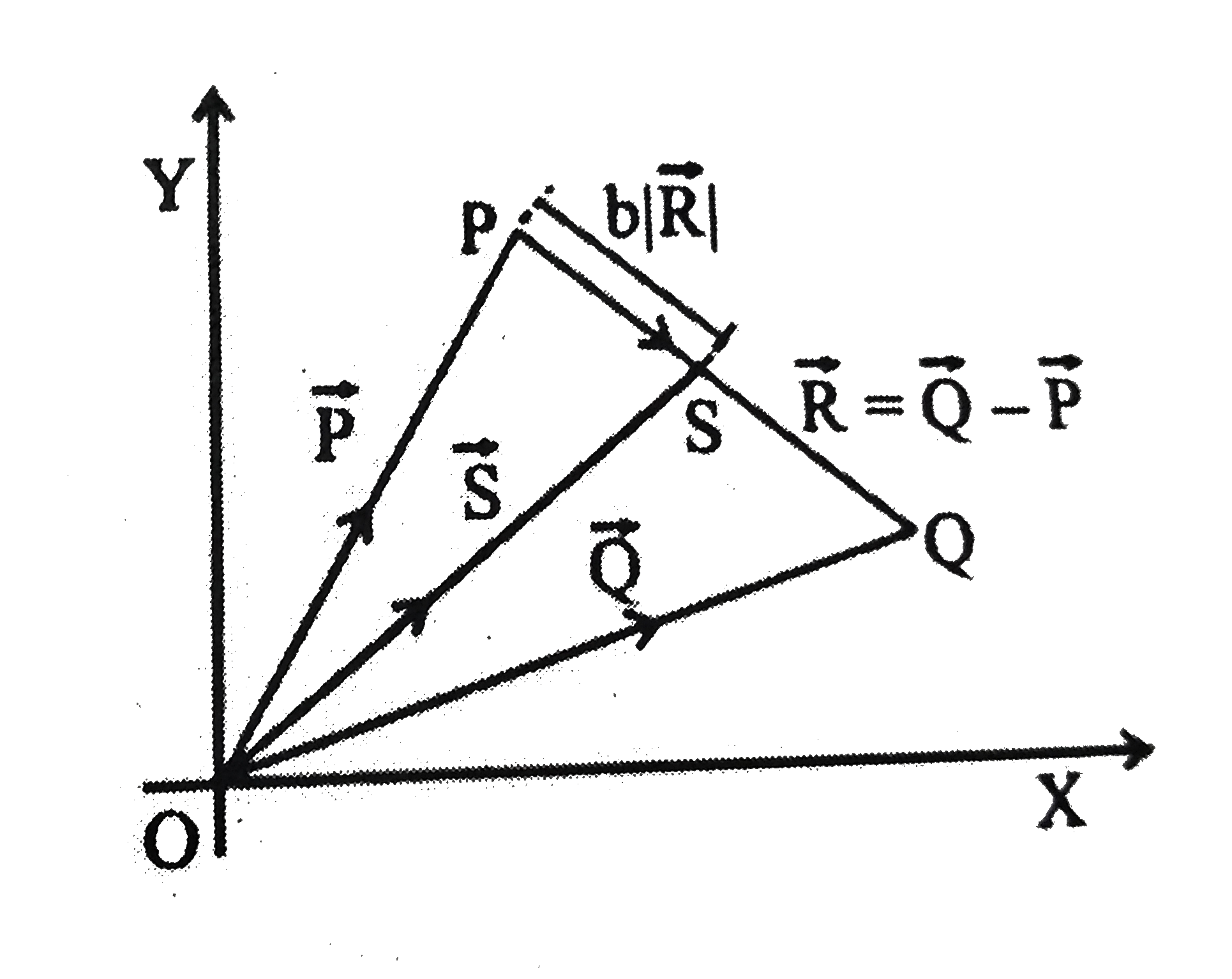
View SolutionSuppose that vec p,vecqand vecr are three non- coplaner in R^(3) ,Let the components of a vector vecs along vecp , vec q and vecr be 4,3, and 5, respectively , if the components this vector vec s along (-vecp+vec q +vecr),(vecp-vecq+vecr) and (-vecp-vecq+vecr) are x, y and z , respectively , then the value of 2x+y+z is
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:

View Solution
