Suppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is Solution in Tamil
The correct Answer is:(9)
(9) According to question →s=4→p+3→q+5→r
and→s=x(−→p+→q+→r)+y(→p−→q+→r)+z(−→p−→q+→r)
∴−x+y−z=4
x−y−z=3
x+y+z=5
Adding (1) and (2) , we get
z=−72
Adding (2) and (3) , we get
x=4
Adding (1) and (3) , we get
y=9/2
∴2x+y+z=2(4)+1=9
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - chapter -2 multiple correct answers type2videos
JEE 2019
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - matching column type2videos
JEE 2019
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Matching coluumn type1videos
JEE 2019
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions529videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Question Bank17videos
LIMITS
Similar Questions
Let →x,→yand→z be three vector each of magnitude √2 and the angle between each pair of them is π3. if →a is a non - zero vector perpendicular to →xand→y×→zand→b is a non-zero vector perpendicular to →yand→z×→x, then
01:45View Solution
03:32View Solution
04:11View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
04:28View SolutionIf Limx→01−cosxeax−bx−1 exist and is equal to 1, then (a2+b2) equals
View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
03:27View SolutionIf vecP+vecQ=vecR" & "vecR is perpendicular to vecP . define angle between vecP" & "vecQ" if " vec|P|=vec|R|-
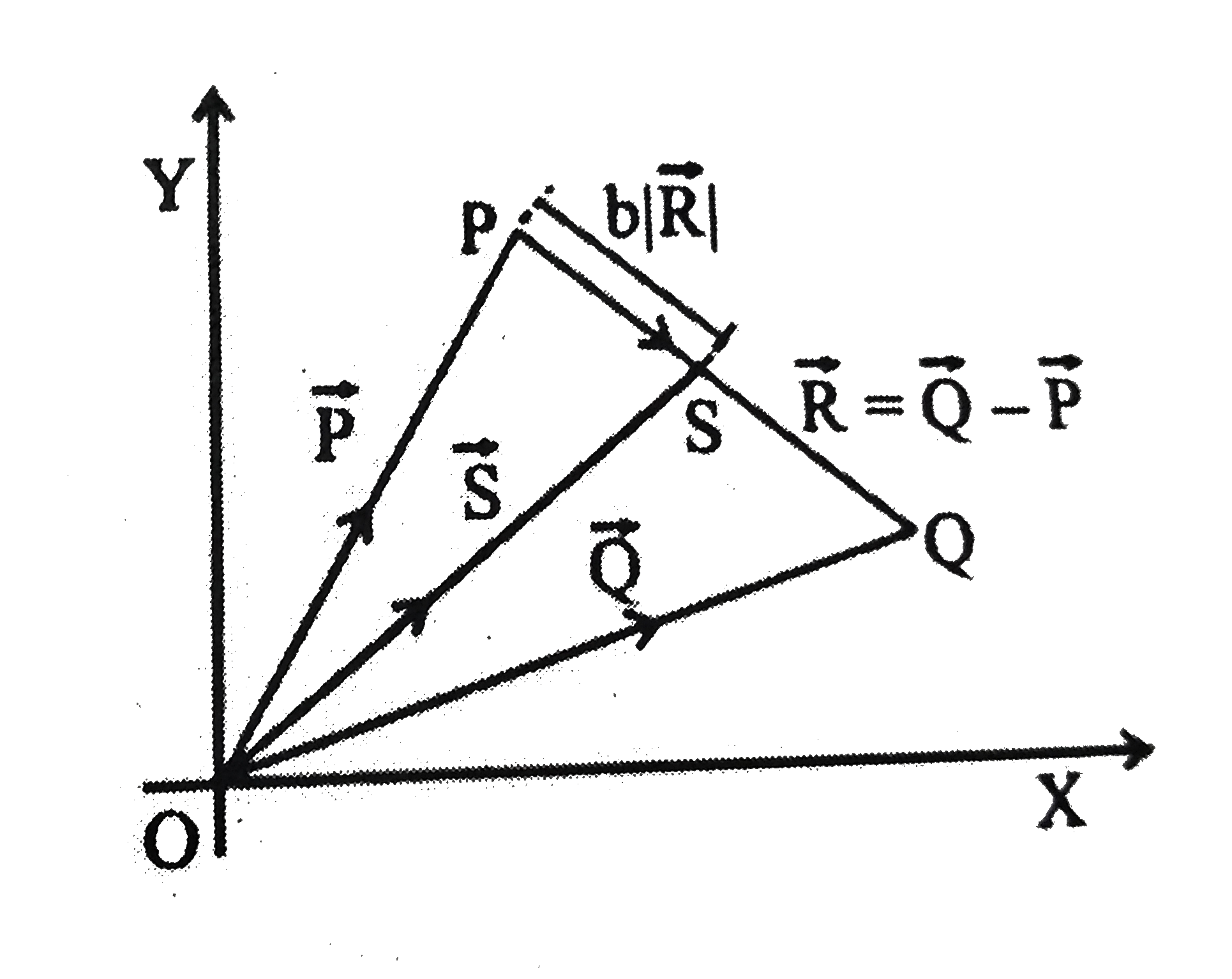
02:22View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
08:21View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
14:24View SolutionSuppose that →p,→qand→r are three non-coplanar vectors in R3. Let the components of a vectors →s along →p,→qand→r be 4, 3 and 5, respectively. If the components of this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x,yandz, respectively, then the value of 2x+y+z is
03:06View SolutionLet →qand→r be non - collinear vectors, If →p is a vector such that →p.(→q+→r)=4and→p×(→q×→r)=(x2−2x+9)→q then +(siny)→r
(x, y) lies on the line03:14View SolutionFor three vectors vecP, vecQ and vecR, vecP+vecQ=vecR and P+Q=R Then prove that vecP and vecQ are parallel to each other.
View SolutionR3 -এর মধ্যে তিনটি অসমতলীয় ভেক্টর হল →p,→q ও→r। মনে করো, →p,→q ও →rভেক্টর তিনটির অভিমুখে →s-ভেক্টরের ভেক্টর উপাংশ 4,3 এবং 5। যদি (−→p+→q+→r),(→p−→q+→r) এবং (−→p−→q+→r) ভেক্টর তিনটির অভিমুখে →s ভেক্টরের ভেক্টর উপাংশ x,y এবং z হয়, তবে 2x+y+z-এর মান নির্ণয় করো।
02:40View SolutionIf →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
03:37View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1 . If →P+→Q−→S=0 angle between →P and →S is θ2 . The ratio of θ1 to θ2 is
02:04View Solution