Let n1<n2<n3<n4<n5 be positive integers such that n1+n2+n3+n4+n5=20. then the number of such distinct arrangements n1,n2,n3,n4,n5 isSolution in Tamil
The correct Answer is:7
PLAN Reducing the equation to a newer equation, where sum of variables is less. Thus, finding the number of arrangements becomes easier.
As n1≥1,n2≥2,n3≥3,n4≥4n5≥5
Let n1−1=x1≥0,n2−2=x2≥0,...,n5−5=x5≥0
⇒ New equation will be
x1+1+x2+2+...+x5+5=20
⇒ x1+x92)+x3+x4+x5)=20−15=5
Now, x1≤x2≤x3≤x4≤x5
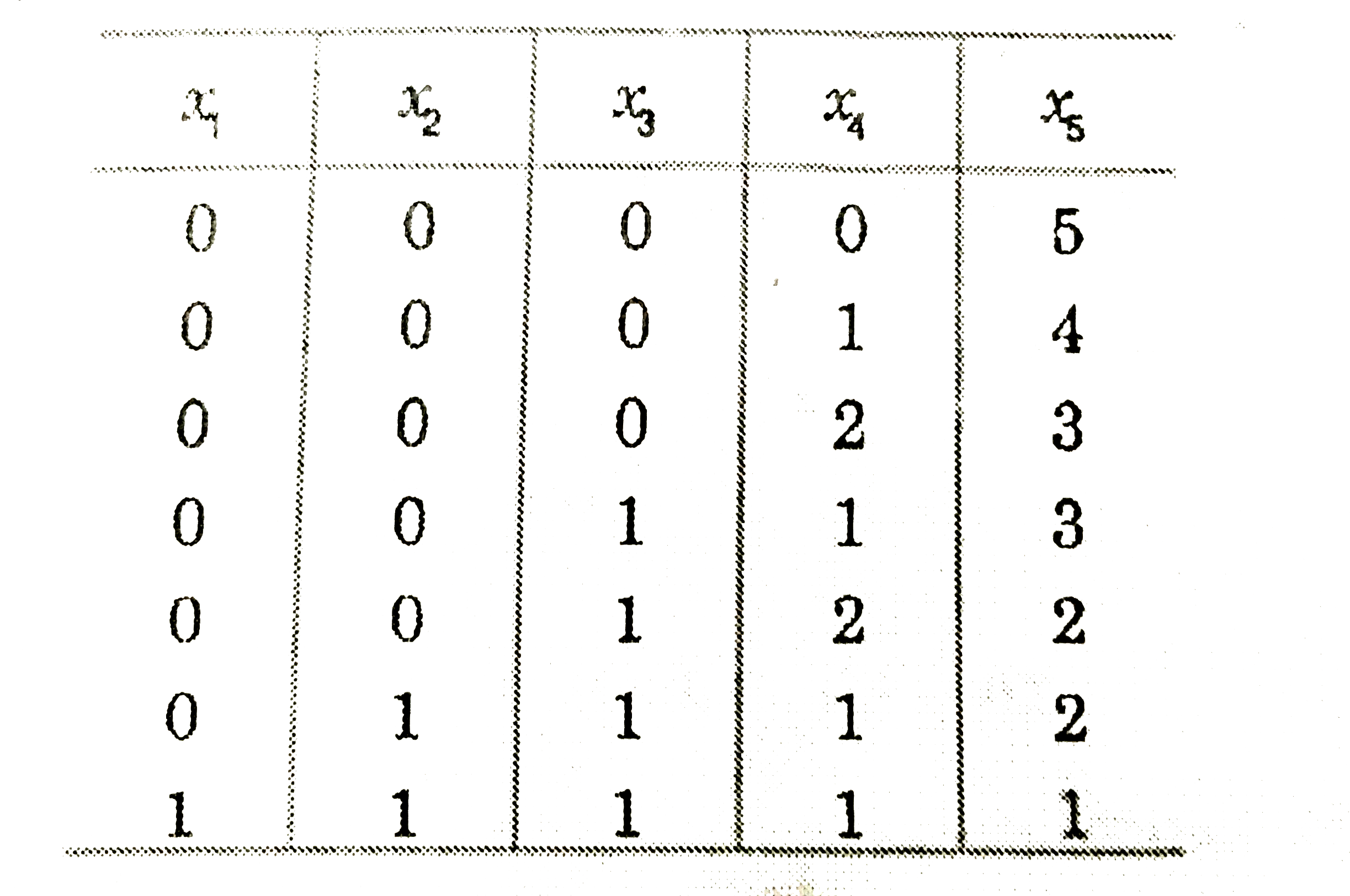
So, 7 possible cases will be there.
Similar Questions
If n_1 lt n_2 lt n_3 lt n_4 lt n_5 There are positive integers of this type for which n_1 +n_2 + n_3+n_4 +n_5=20 is . Then such distinct arrangements (n_1 , n_2 , n_3 , n_4 ,n_5) Is the total number of
View SolutionConsider the set A={3,4,5} and the number of null relations, identity relation, universal relations,reflexive relation on A are respectively n1,n2,n3,n4,Then the value of n1+n2+n3+n4 is equal to
View SolutionWhich of the follawing transition will have minimum wavelength? n4→n1, n2→n1, n4→n2, n3→n1
View SolutionIf S1,S2 and S3 denote the sum of first n1,n2 and n3 terms respectively of an A.P. Then S1n1(n2−n3)+S2n2(n3−n1)+S3n3(n1−n2) equals :
View Solutionn1,n2,n3,n4 রাশিগুলির গড় 10 হলে,n1+4,n2+4,n3+4,n4+4 রাশিগুলির গড় হবে –
View SolutionThe value of cos2100−cos100cos500+cos2500 is equal to 43 (b) 13 (c) 34 (d) 3
View SolutionIf (sin−1x+sin−1w)(sin−1y+sin−1z)=π2, then D=∣∣xN1yN3zN3wN4∣∣(N1,N2,N3,N4∈N)
View SolutionLet n1<n2<n3<n4<n5 be positive integers such that n1+n2+n3+n4+n5=20. then the number of distinct arrangements n1,n2,n3,n4,n5 is
View Solution