Four numbers n1,n2,n3andn4 are given as n1=sin15∘−cos15∘,n2=cos93∘+sin93∘,n3=tan27∘−cot27∘,n4=cot127∘+tan127∘,Then
A
n1<0
B
n2<0
C
n3<0
D
n4<0
Video Solution
Text Solution
The correct Answer is:A, C, D
n1=sin15∘−cos15∘<−ve (cos15∘>sin15∘)
n2=cos93∘+sin93∘
=−sin3∘+cos3∘>0 (cos3∘>sin3∘)
n3=tan27∘−cot27∘<0 (tan27∘<cot27∘)
n4=cot127∘+tan127∘<0 (tan127∘,cot127∘<0).
|
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Comprehension)
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Matrix)
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Single)
57 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
Knowledge Check
The value of cosn38∘−cotn52∘sinn52∘−tann38∘=?
A5B7C1D3The value of cotn29∘−cotn61∘tann61∘−tann29∘=?
A5B7C1D3
tan−1n+cot−1(n+1)=tan−1(n2+n+1)
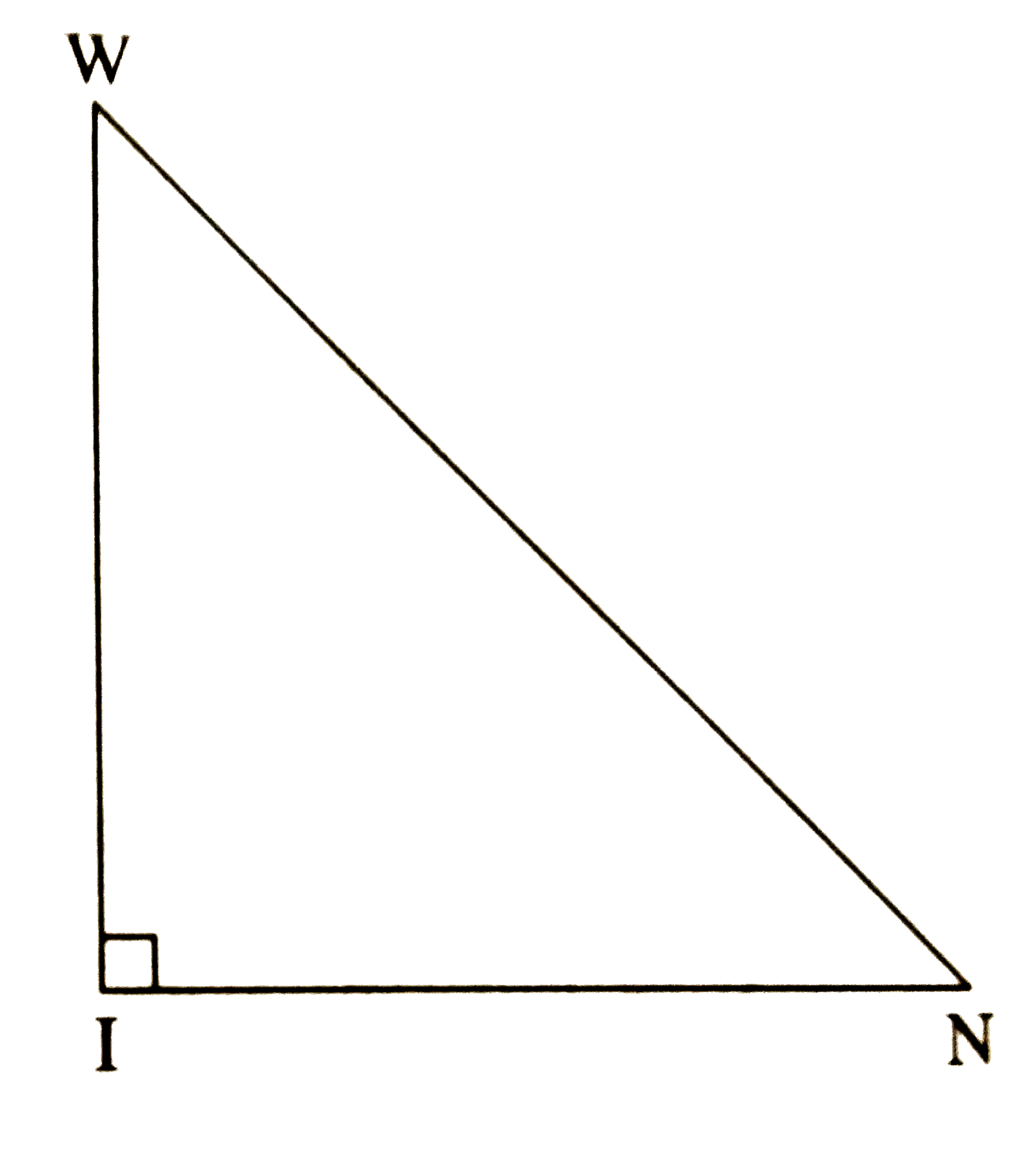
View SolutionIn the figure , find sin N ,
cos N, tan W and sin W.
View SolutiontanA+2tan2A+.....+2n−1tan2n−1A+2ncot2nA=
View SolutionIf tanB=nsinA.cosA1−nsin2A, then prove that tan(A−B)=(1−n)tanA.
View SolutionIf x∈R and n∈I then the determinant Δ=∣∣ ∣ ∣ ∣∣sin(nπ)sinx−cosxlogtanxcosx−sinxcos{(2n+1)π2}logcotxlogcotxlogtanxtan(nπ)∣∣ ∣ ∣ ∣∣=
View SolutionProvethat the average of the numbers nsinn∘, n = 2,4,6...180 is cot1∘
View Solution
