A circle centred at 'O' has radius 1 and contains the point A. Segment AB is tangent to the circle at A and ∠AOB=θ. If point C lies on OA and BC bisects the angle ABO then OC equals
secθ(secθ−tanθ)
cos2θ1+sinθ
11+sinθ
1−sinθcos2θ
The correct Answer is:A, B, D
Using property of angle bisector, we get
OBAB=OCAC⇒secθtanθ=x1−x
orx=secθsecθ+tanθ
xsecθ(secθ−tanθ)=11+sinθ

Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Comprehension)
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Matrix)
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Single)
57 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
A circle centred at O has radius 1 and contains the point A. Segment AB is tangent to the circle at A and angle AOB=θ.If point C lies on OA and BC bisects the angle ABO then OC equals
View SolutionA circle centred at O has radius 1 and contains the point A. Segment AB is tangent to the circle at A and angle AOB=θ.If point C lies on OA and BC bisects the angle ABO then OC equals
View Solution
Knowledge Check
In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
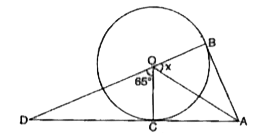 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘PA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
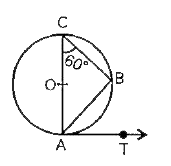 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘
A circle centred at 'O' has radius 1 and contains the point A. Segment AB is tangent to the circle at A and ∠AOB=θ. If point C lies on OA and BC bisects the angle ABO then OC equals
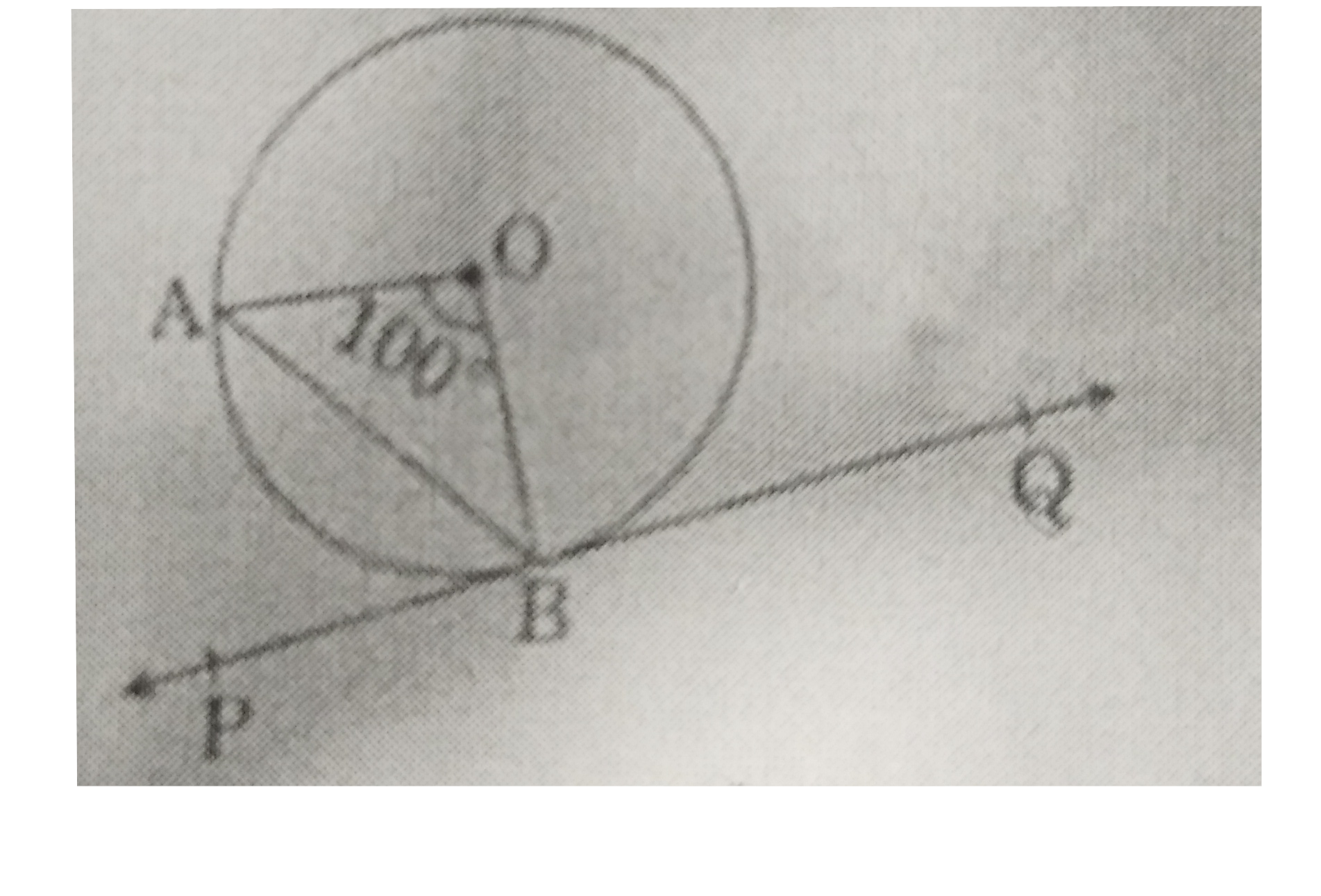
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn the given, figure , O is the centre of the circle and AD is a tangent to the circle at.A if ∠CAD=55∘ and ∠ADC=25∘, then find ∠ABO.

View SolutionThe congruent circles with centres Oand O' intersect at two points A and B. Then, ∠AOB=∠AO'B.
View Solution
