If px+qx+r=0 represent a family fo staright lines such that 3p+2q+4r=0 then (a) All lines are parallel (b) All lines are incosistance (c) All lines are concurrent at (34,12) (d) All lines are concurrent at (3,2) Solution in Tamil
Each lines passes through the origin.
The lines are concurrent at the point (34,12)
The lines are all parallel
The lines are not concurrent
Given, px+qy+r=0 is the equation of line such that 3p+2q+4r=0
Consider, 3p+2q+4r=0
⇒3p4+2q4+r=0 (dividing the equation by 4)
⇒p(34)+q(12)+r=0
⇒(34,12) satisfy px+qy+r=0
So, the lines always passes through the point (34,12).
Similar Questions
Consider the set of all lines px+qy+r=0 such that 3p+2q+4r=0. Which one of the following statements is true ?
View SolutionThe lines px+qy+r=0,qx+ry+p=0,rx+py+q=0, are concurrant then
View SolutionThree lines px + qy + r = 0, qx + ry + p = 0 and rx + py + q = 0 will be concurrent, if -
View SolutionFrom the given figure, write
(i) all pairs of parallel lines
(ii) all pairs of intersecting lines
(iii) concurrent lines and point of concurrence
(iv) collinear points
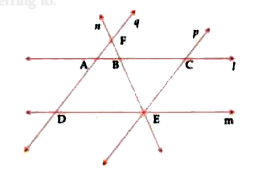
View SolutionIn the adjoining figure write.
(i) all pairs of parallel lines
(ii) all pairs of intersecting lines.
(iii) Concurrent lines.
(iv) Collinear points.
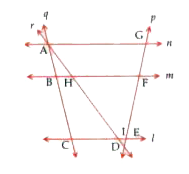
View SolutionLimes p,q and r are concurrent . Lines q,r and s are also concurrent . Will all the four lines p,q,r and s be concurrent ?
View SolutionIf a,b,c are arithmetic progression then show that the equation ax+by+c=0 represents a family of concurrent lines and find the point of concurrency.
View SolutionThe lines px+qy+r=0,qx+ry+p=0,rx+py+q=0, are concurrant then
View Solution