A rectangle PQRS has its side PQ parallel to the line y=mx and vertices P,QandS on the lines y=a,x=b, and x=−b, respectively. Find the locus of the vertex R.Solution in Tamil
Let the coordinates of Q be (b,α) and that of S be (−b,β). Suppose , PR and SQ meet in G. Since, G is mid-point of SQ, its x-coordinate must be 0. Let the coordinates of R be (h,k).
Since G, is mid point of PR, the x-coordinate at P must be −h and as P lies on the line y=a, the coordinates of P are (−h,a). Since , PQ is parallel to y=mx, slope of PQ=m
⇒α−ab+h=m.........(i)
Again RQ⊥PQ
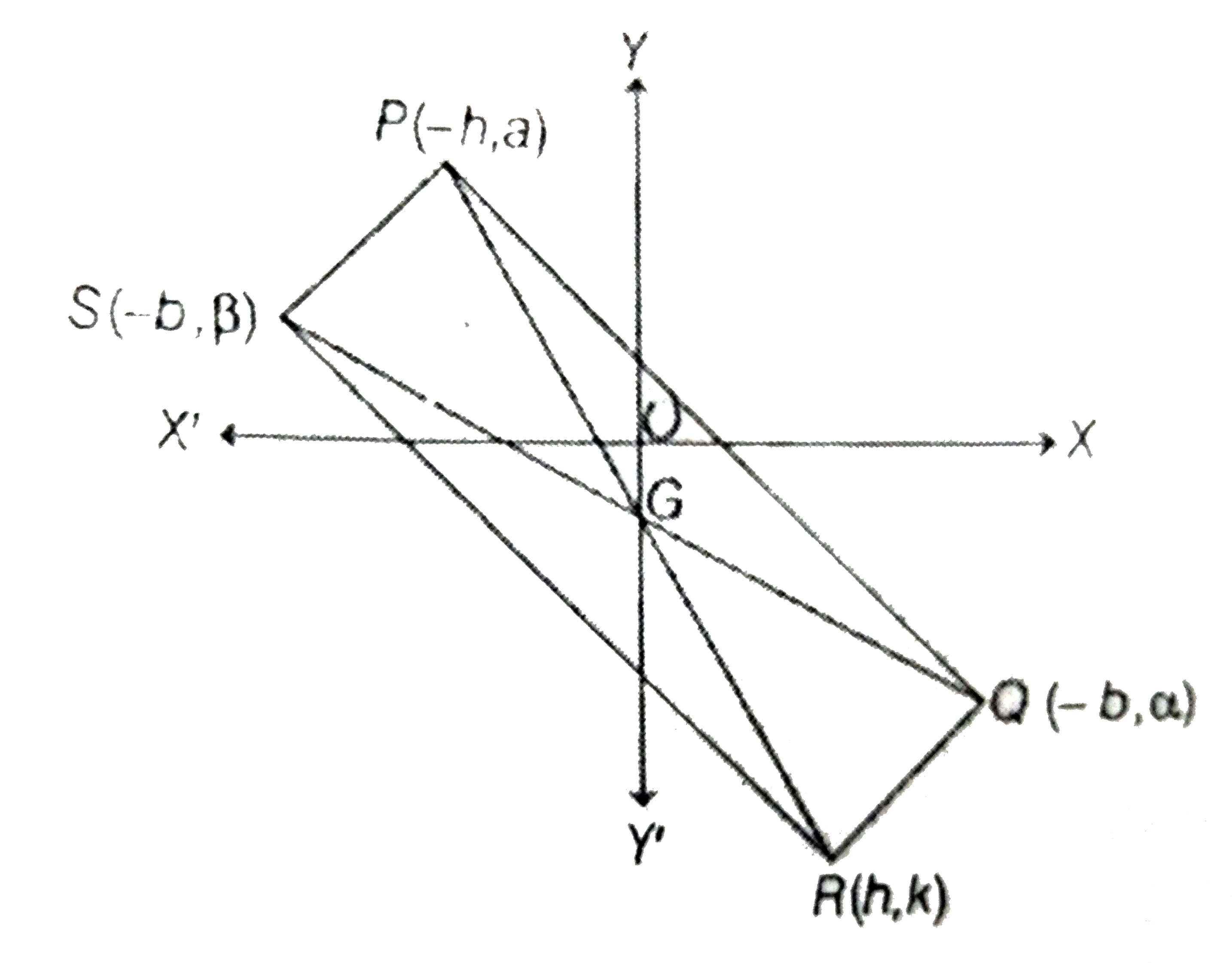
Slope of RQ=−1m⇒k−αh−b=−1m.........(ii)
From Eq. (i), we get
α−a=m(b+h)
⇒α=a+m(b+h)..........(iii)
and from Eq. (ii), we get
k−α=−1m(h−b)
⇒α=k+1m(h−b).......(iv)
From Eqs. (iii) and (iv) , we get
a+m(b+h)=k+1m(h−b)
⇒am+m2(b+h)=km+(h−b)
⇒(m2−1)h−mk+b(m2+1)+am=0
Hence, the locus of vertex is
(m2−1)x−my+b(m2+1)+am=0
Similar Questions
The image of P(a,b) on the line y=−x is Q and the image of Q on the line y=x is 'R' find the mid-point of 'P' and 'R'
View SolutionA rectangle ABCD has its side AB parallel to line y=x, and vertices A,B and D lie on y=1, x=2 and x=-2 respectively. The locus of vertex C is
View SolutionThe lines (p-q)x+(q-r)y+(r-p)=0(q-r)x+(r-p)y+(p-q)=0 (r-p)x+(p-q)y+(q-r)=0
View SolutionA rectangle PQRS has its side PQ parallel to the line y= mx and vertices P,Q and S on the lines y = a, x= b and x = -b respectively, Find the locus of the vertex R.
View SolutionIf ∣∣ ∣ ∣∣a−bb−cc−ax−yy−zz−xp−qq−rr−p∣∣ ∣ ∣∣=m∣∣ ∣ ∣∣cabzxyrpq∣∣ ∣ ∣∣, then m=
View SolutionA rectangle PQRS has its side PQ parallel to the line y= mx and vertices P, Q , and S on the lines y= a, x=b ,and x= - b , respectively. Find the locus of the vertex R .
View SolutionThe image of P(a,b) on the line y=-x is Q and the image of Q on the line y=x is R find the mid-point of P and R
View SolutionA rectangle PQRS has its side PQ parallel to the line y= mx and vertices P,Q, and S on the lines y=a, x=b, and x=-b, respectively. Find the locus of the vertex R.
View Solution