Question

A rectangle PQRS has its side PQ parallel to the line $y=mx$ and vertices $P,Q$, and $S$ on the lines $y=a,x=b$,and $x=-b$, respectively. Find the locus of the vertex $R$.

Explanation

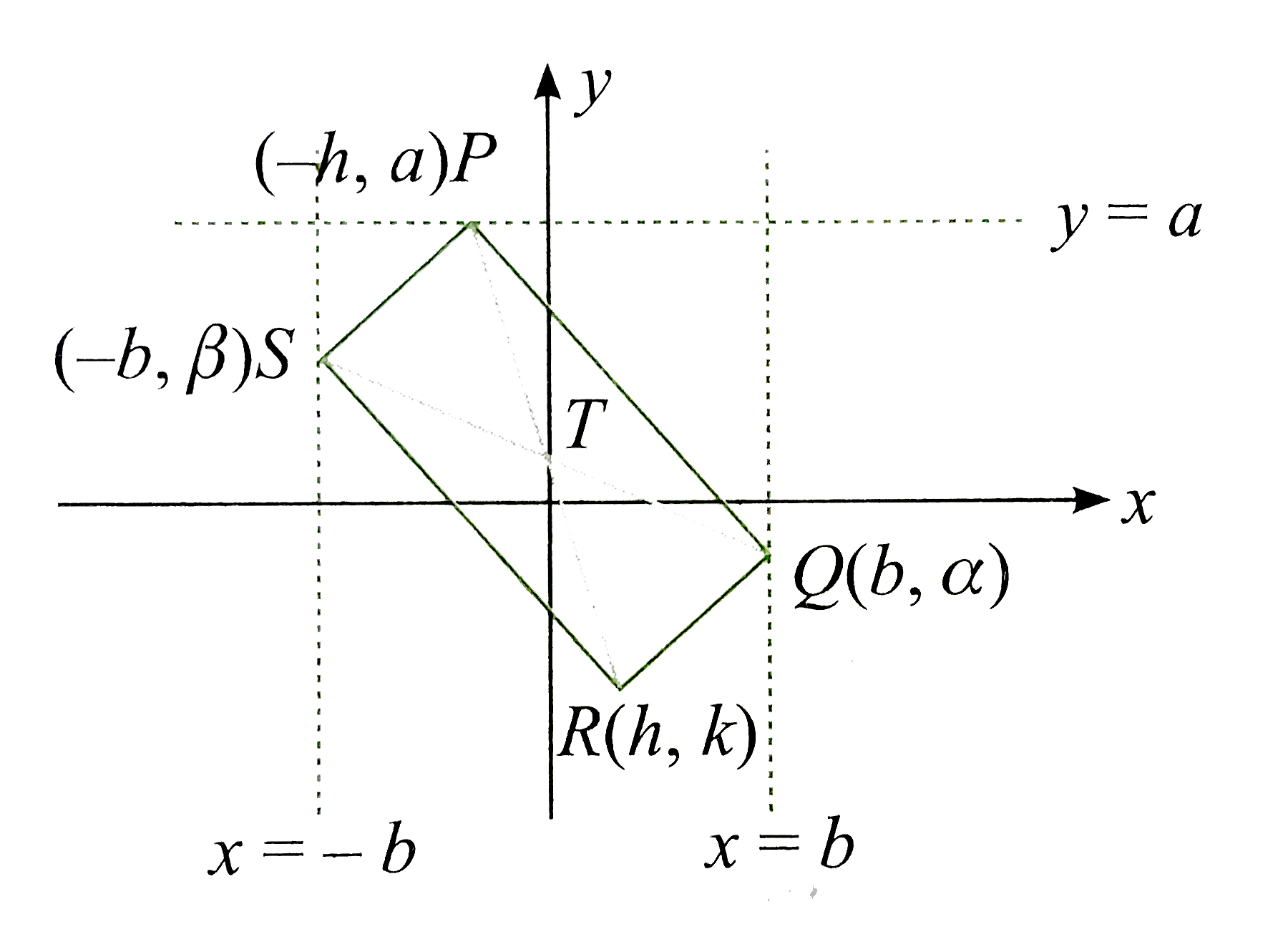
Let the coordinates of Q be `(b, alpha)` and that of S be `(-b, beta)`.
Let PR and SQ intersect each other at T.
`therefore " T is the mid point of SQ "`
Since diagonal of a rectangle bisect each other, x co-ordinates of Pis -h.
As P lies on y=a, therefore coordinates of Pare (-h,a).
Given that PQ is parallel to y=mx and slope of PQ = m.
`therefore (alpha-a)/(b+h) = m`
`rArr alpha = a +m(b+h) " " (1)`
`"Also", RQ bot PQ rArr "slope of " RQ = (-1)/(m)`
`therefore (k-alpha)/(h-b) = (-1)/(m) rArr alpha = k + (1)/(m)(h-b) " " (2)`
From (1) and (2), we get
`a+m(b+h)=k+(1)/(m)(h-b)`
`rArr am+m^(2) (b+h) = km +(h-b)`
`rArr (m^(2)-1)h-mk+b(m^(2)+1) +am=0`
Therefore, locus of (h,k) is
`(m^(2)-1)x-my+b(m^(2)+1) +am =0`