Find the area of the greatest rectangle that can be inscribed in the ellipse x2a2+y2b2=1.Solution in Tamil
Reactangle can be inscribed in the ellipse with its sides parallel ot axes of theellipse as shown in the following figure.
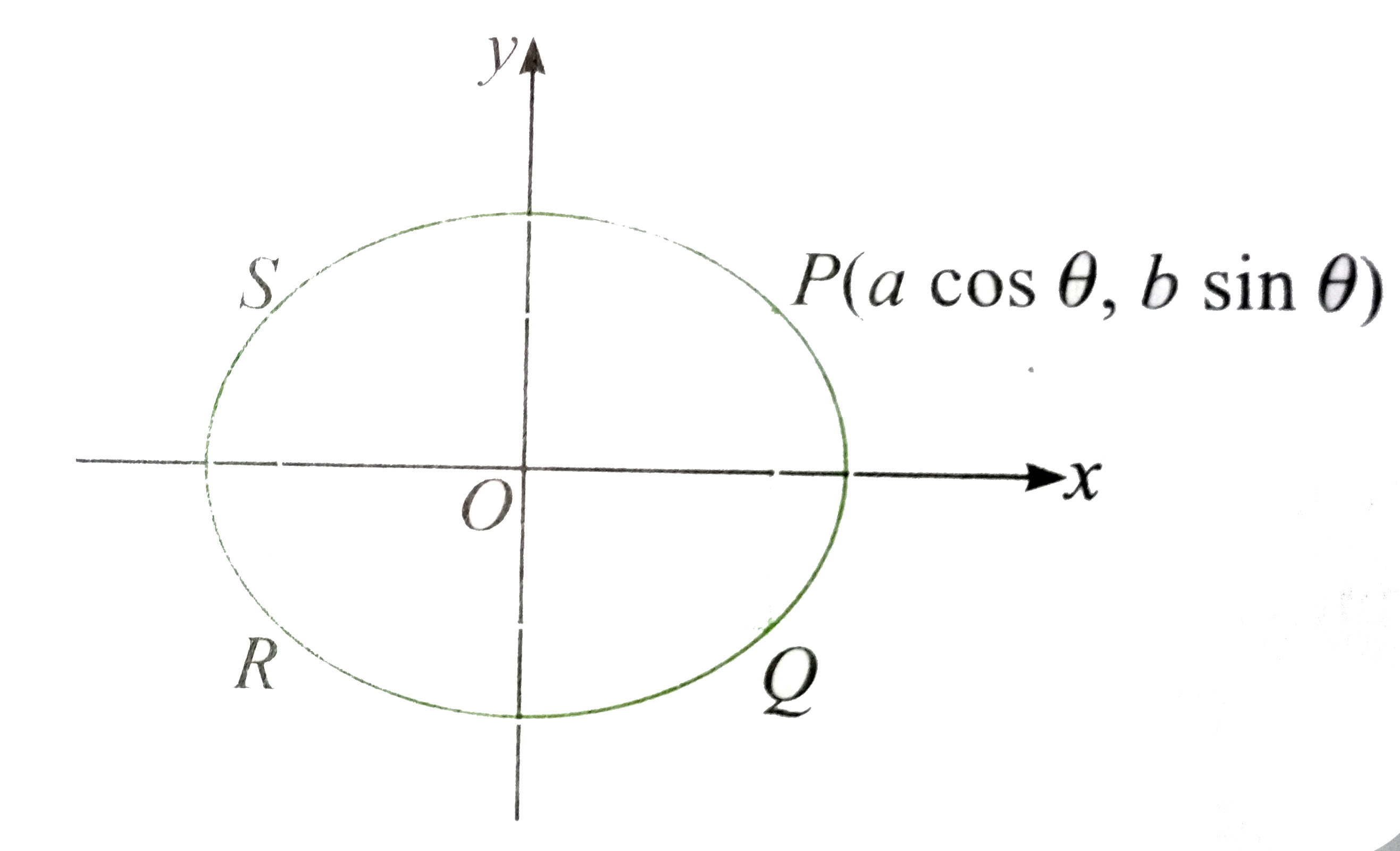
Let P≡(acosθ,bsinθ)
∴ Area o reactangle PQRS
=(2acosθ)(2bsinθ)
=2absin2θ
This is maximum when sin2θ=1
Henece, maximum area =2ab(1)=2ab
Similar Questions
Find the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1
View SolutionFind the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionFind the area of greatest rectangle that can be inscribed in x2a2+y2b2=1.
View SolutionFind the greatest rectangle that can be inscribed in x2a2+y2b2=1
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionFind the area of greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1.
View Solution
