Find the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1
Reactangle can be inscribed in the ellipse with its sides parallel ot axes of theellipse as shown in the following figure.
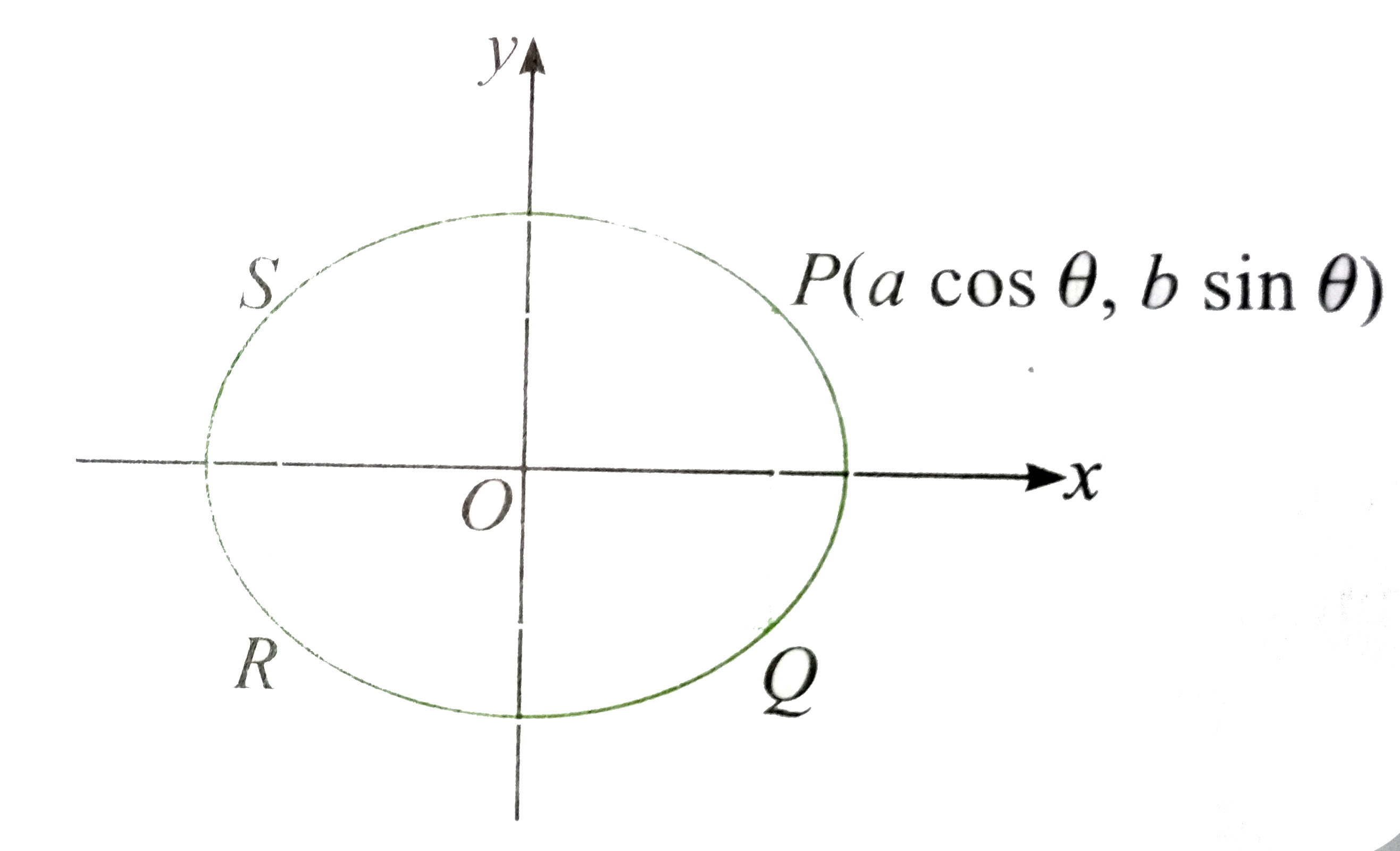
Let P≡(acosθ,bsinθ)
∴ Area o reactangle PQRS
=(2acosθ)(2bsinθ)
=2absin2θ
This is maximum when sin2θ=1
Henece, maximum area =2ab(1)=2ab
Topper's Solved these Questions
Similar Questions
Find the area of the greatest isosceles triangle that can be inscribed in the ellipse (x2a2)+(y2b2)=1 having its vertex coincident with one extremity of the major axis.
View SolutionFind the area enclosed by the ellipse x2a2+y2b2=1.
View SolutionFind the maximum area of an isosceles triangle inscribed in the ellipse x2a2+y2b2=1with its vertex at one end of the major axis.
View SolutionAn isosceles triangle that can be inscribed in an ellipse x2a2+y2b2=1 having its vertex coincident with one extremity of major axis has the maximum area equal to m√n4ab (m,n are prime numbers) then m2−n3=
View SolutionThe area of the ellipse x2a2+y2b2=1 is
View SolutionFind the equation of the largest circle with centre (1, 0) that can be inscribed in the ellipse x2+4y2=16
View SolutionIf A be the area of the largest circle with centre (1,0) that can be inscribed in the ellipse x2+4y2=16, then 945πA=.
View SolutionThe dimension of the rectangle of maximum area that can be inscribed in the ellipse (x/4)2+(y/3)2=1 are
View SolutionFind the eccentric angles of the extremities of the latus recta of the ellipse x2a2+y2b2=1
View SolutionFind the locus of the vertices of equilateral triangle circumscribing the ellipse x2a2+y2b2=1.
View Solution
