A line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.Solution in Tamil
Let R≡(h,k)
From the fiugure,
h=acosθ
and k=bsinθ
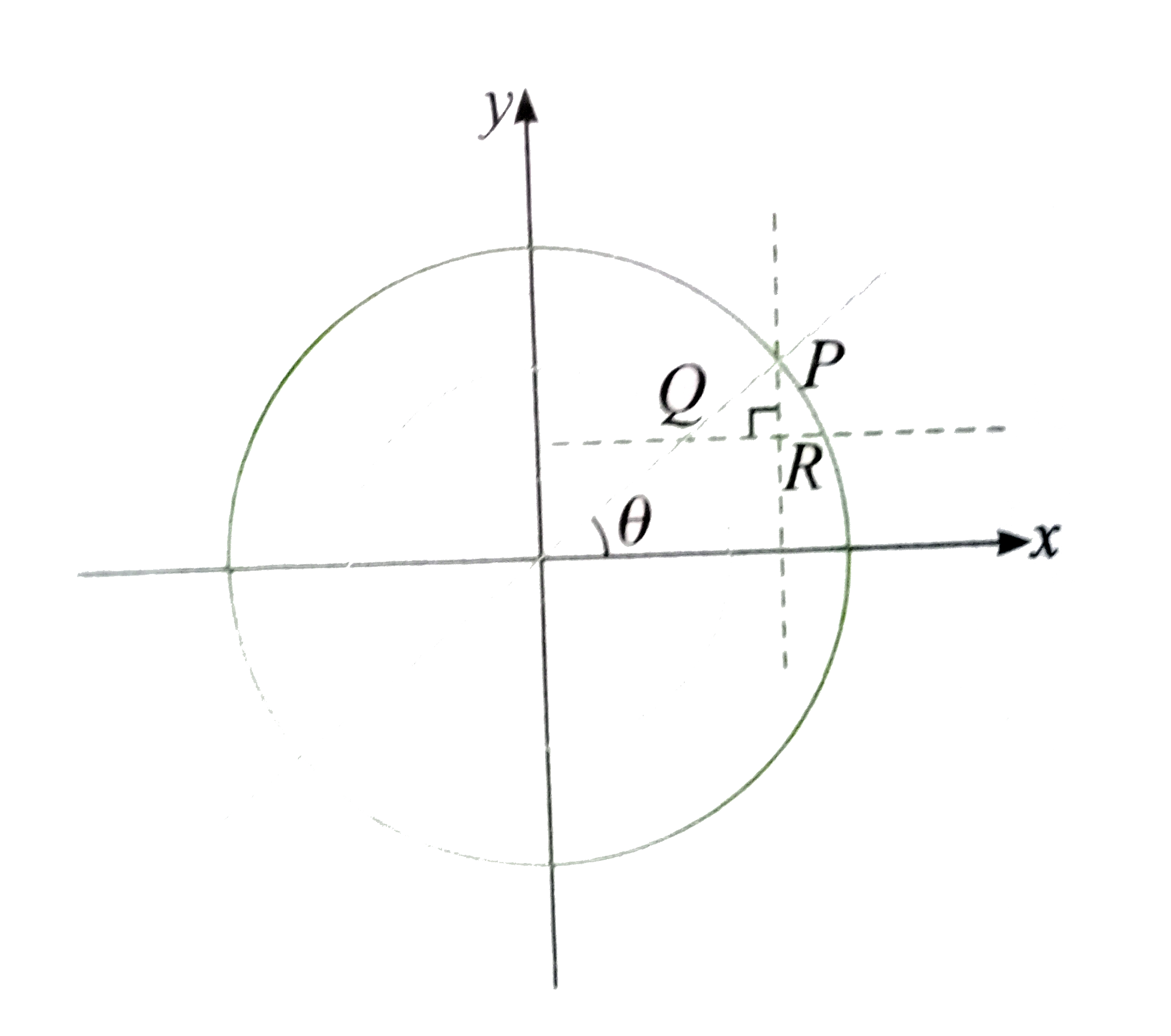
Squaring and adding, we get
h2a2+k2b2=1
So, x2a2+y2b2=1 is required locus.
Similar Questions
The straight line xa+yb=1 cuts the coordinate axes at A and B . Find the equation of the circle passing through O(0,0),AandB.
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View SolutionA variable line through the point P(2,1) meets the axes at AandB . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionA straight line is drawn through P(3,4) to meet the axis of x and y at AandB , respectively. If the rectangle OACB is completed, then find the locus of C.
View SolutionA variable line through point P(2,1) meets the axes at AandB . Find the locus of the circumcenter of triangle OAB (where O is the origin).
View SolutionTwo circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.
View SolutionA line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.
View SolutionA straight line is drawn through P(3,4) to meet the axis of x and y at Aa n dB , respectively. If the rectangle O A C B is completed, then find the locus of Cdot
View Solution
