Two circles passing through A(1,2),B(2,1) touch the line 4x+8y−7=0 at C and D such that ACED in a parallelogram. Then: coordinates of E areSolution in Tamil
The midpoint of AE must be the point of intersection of diagonals of parallelogram.
Let E≡(h,k).
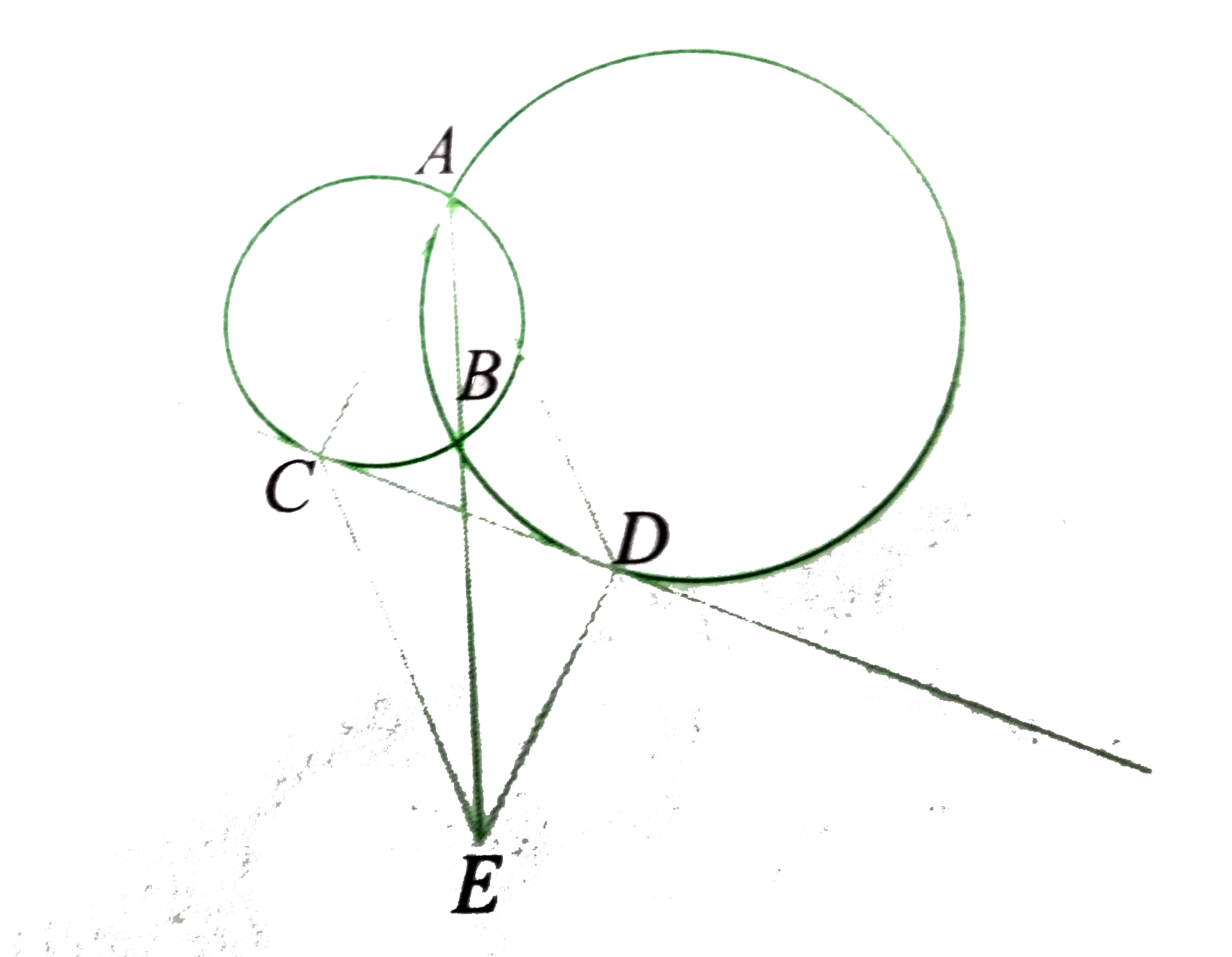
So, (h+12,k+22) must lie on common tangent 4x+8y−7=0.
∴2h+4k+3=0 (1)
Also, (h,k) lies on AB whose equation is x+y=3.
∴h+k=3 (2)
Solving (1) and (2) , we get
h=152,k=−92
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionTwo circles C1andC2 both pass through the points A(1,2)andE(2,1) and touch the line 4x−2y=9 at BandD, respectively. The possible coordinates of a point C, such that the quadrilateral ABCD is a parallelogram, are (a,b). Then the value of |ab| is_________
View SolutionTwo circles passing through A(1,2),B(2,1) touch the line 4x+8y-7=0 at C and D such that ACED in a parallelogram.Then:
View SolutionEquation of the circle which touches the coordinate axes and passes through the point (2,1) is
View SolutionEquation of circle passing through A(-1,-3), B (3,0)
and touching line 4x+3y−12=0 at B , is
View SolutionThe equation of the circle passing through (2,1) and touching the coordinate axes is
View SolutionThe equation to the circles which touch the lines 3x-4y+1=0, 4x+3y-7=0 and pass through (2,3) are
View SolutionShow that the tangent at (−1,2) of the
circle x2+y2−4x−8y+7=0
touches
the circle x2+y2+4x+6y=0 and also
find its point of contact.
View SolutionThe equation of the circle passing through (2,1) and touching the coordinate axes is
View SolutionThe common chord of the circle x2+y2+6x+8y−7=0 and a circle passing through the origin and touching the line y=x always passes through the point. (a) (−12,12) (b) (1, 1) (c) (12,12) (d) none of these
View SolutionTwo circles C1andC2 both pass through the points A(1,2)andE(2,1) and touch the line 4x−2y=9 at BandD, respectively. The possible coordinates of a point C, such that the quadrilateral ABCD is a parallelogram, are (a,b). Then the value of |ab| is_________
View SolutionTwo circles passing through A(1,2),B(2,1) touch the line 4x+8y−7=0 at C and D such that ACED in a parallelogram. Then:
View Solution
