At a point P on the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ tangents PQ is drawn. If the point Q be at a distance $\frac{1}{p}$ from the point P, where 'p' is distance of the tangent from the origin, then the locus of the point Q is Solution in Tamil

A

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 + \frac{1}{a^{2} b^{2}}$

B

$\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 - \frac{1}{a^{2} b^{2}}$

C

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = \frac{1}{a^{2} b^{2}}$

D

$\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = \frac{1}{a^{2} b^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation of the tangent at P is
$\frac{x - a cos θ}{a sin θ} = \frac{y - b sin θ}{- b cos θ}$

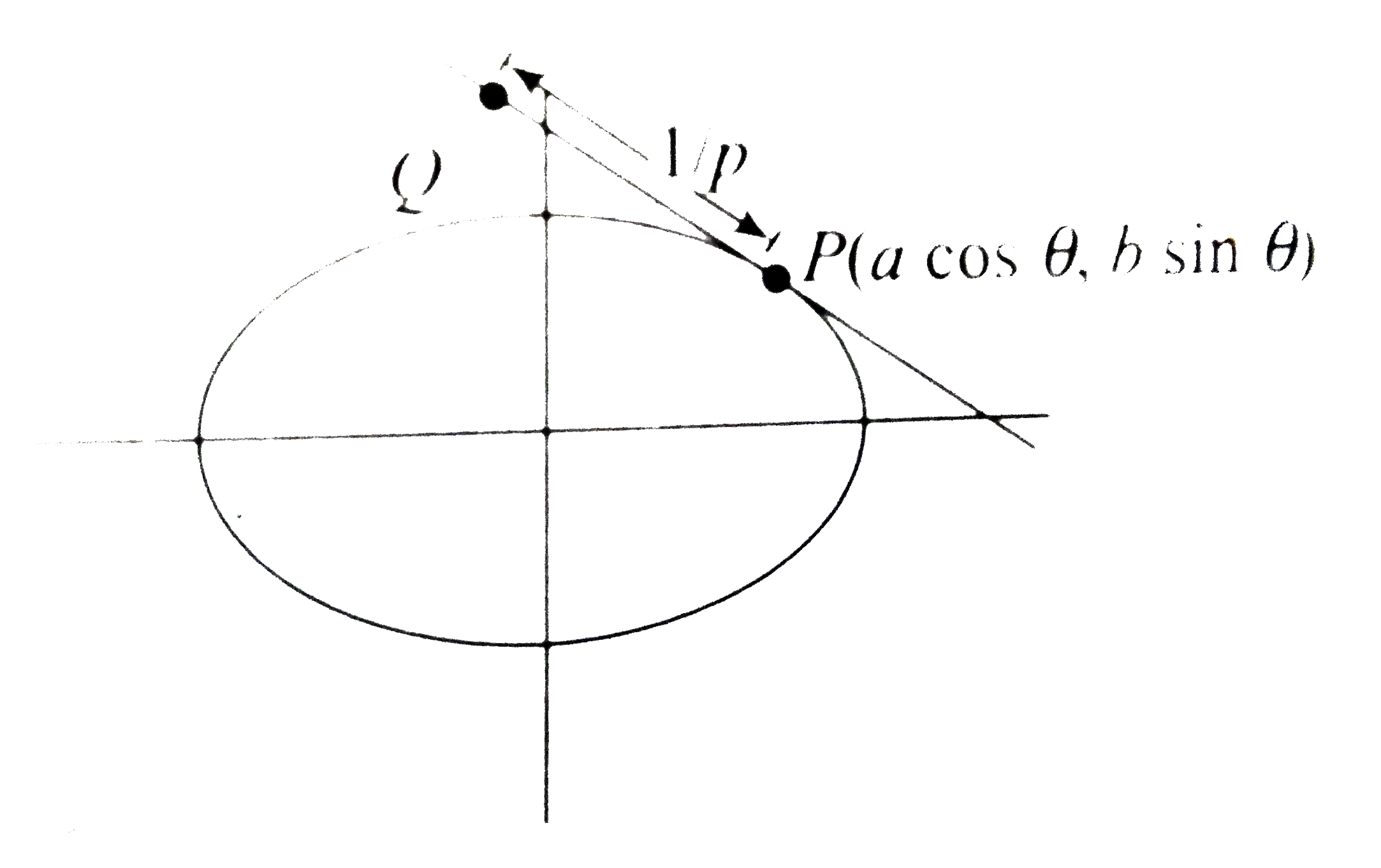
The distance of the tangent from the origin is
$p = ∣ ∣ ∣ ∣ \frac{a b}{\sqrt{b^{2} {cos}^{2} θ + a^{2} {sin}^{2} θ}} ∣ ∣ ∣ ∣$
$\Rightarrow \frac{1}{p} = \frac{\sqrt{b^{2} {cos}^{2} θ + a^{2} {sin}^{2} θ}}{a b}$
Now the coordinates of the point Q are given as follows
$\frac{\frac{x - a cos θ}{- a sin θ}}{\sqrt{b^{2} {cos}^{2} θ + a^{2} {sin}^{2} θ}} = \frac{\frac{y - b sin θ}{b cos θ}}{\sqrt{b^{2} {cos}^{2} θ + a^{2} {sin}^{2} θ}} = \frac{1}{p} = \frac{\sqrt{b^{2} {cos}^{2} θ + a^{2} {sin}^{2} θ}}{a b}$
$\Rightarrow x = a cos θ - \frac{a sin θ}{a b}$ and $y = b sin θ \frac{b cos θ}{a b}$
$\Rightarrow {(\frac{x}{a})}^{2} + {(\frac{y}{b})}^{2} = 1 + \frac{1}{a^{2} b^{2}}$ is the required locus.

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

CENGAGE-ELLIPSE -Multiple Correct Answers Type

Home
Ask Doubt
Profile