In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then Solution in Tamil
locus of P is an ellipse with eccentricity √23
locus of P is a hyperbola with eccentricity √32
area of the quadr5ilateral ABCD=163 sq. units
area of the quadrilateral ABCD=323 sq. units
The correct Answer is:A, C
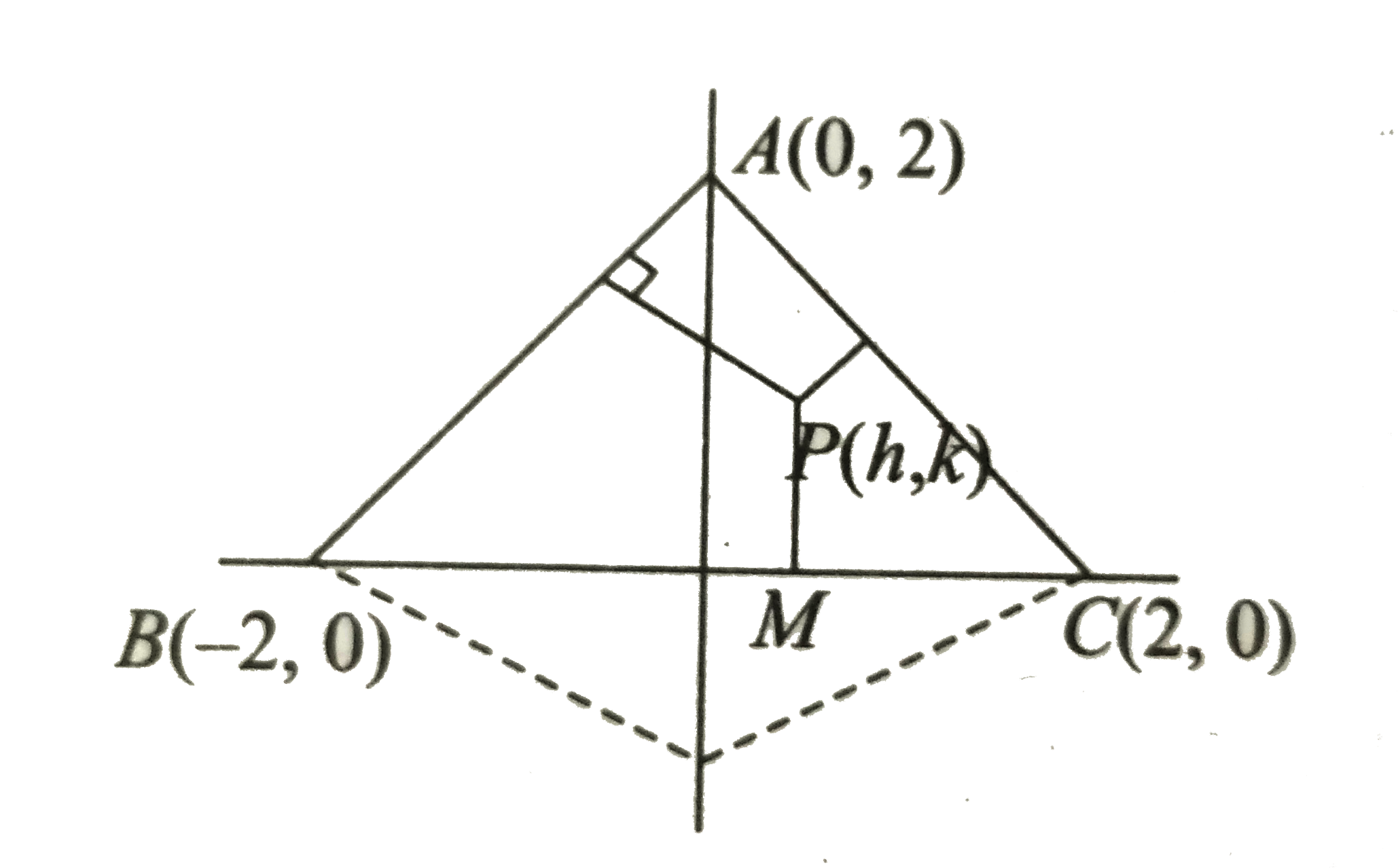
PM=k
Equation of AB≡x+y=2
Equation of AC≡x+y=2
According to question
(2−h−k√2)(2+h+k√2)=2k2
⇒h2+3k2+4k=4
⇒h2+3(k2+43k+49)=4+43
⇒h2+3(k+23)2=163⇒h216/3+(k+23)216/9=1
⇒ Ellipse with e=√23 and D≡(0,−23).
Topper's Solved these Questions
Similar Questions
Let a,b>0 and →α=(→ia+4ˆjb+bˆk) and →β=bˆi+aˆj+1bˆk, then the maximum value of 305+→α.→β is
View SolutionLet any double ordinate PNP' of the hyperbola x225−y216=1 be produced on both sides to meet the asymptotes in QandQ' . Then PQ.P′Q is equal to 25 (b) 16 (c) 41 (d) none of these
View SolutionABCD is a square with side AB=2. A point P moves such that its distance from A equals its distance from the line BD.The locus of P meets the line AC at T_(1) and the line through A parallel to BD at T_(2) and T_(3). The area of the triangle T_(1)T_(2)T_(3) is :
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View SolutionABC is an isosceles triangle with its base BC twice its altitude.A polnt P moves within the triangle such that the square of its distance from BC is half the rectangle contained by its distances from the two sides.Show that the locus of P is an ellipse with eccentricity sqrt((2)/(3)) passing through B&C.
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length a of a rectangle is twice the sum of the squares of its distances from the other two sides of length b.The locus of the point can be:
View SolutionIn triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
View SolutionThe point P moves such that the sum of the squares of its distances from two fixed points A(a,0)andB(−a,0) is constant and equal to 6a2. The locus of P is
View SolutionIf A(−2,1),B(0,−2),C(1,2) are the vertices of a triangle ABC, then the perpendicular distance from its circumcentre to the side BC is
View SolutionIf A(-2,1), B(0,-2), C(1,2) are the vertices of a triangle ABC , then the perpendicular distance from its circumference of the side BC is ,
View SolutionStatement 1: In a triangle ABC , If base BC is fixed and perimeter of the triangle is constant, then vertex A moves on an Ellipse.
Statement 2: If the sum of distances of a point P from two fixed points
is constant then locus of P is a real ellipse
View SolutionIn triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View SolutionThe point P moves such that the sum of the squares of its distances from two fixed points A(a,0),B(−a,0) is 8a2 the locus of P is
View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें आधार BC इसकी ऊँचाई का दुगना है। एक बिन्दु,त्रिभुजके अन्दर इस प्रकार गमन करता है कि BC से इसकी दूरी का वर्ग, त्रिभुज की दो समान भुजाओं तथा से डाले गए लम्बों द्वारा बने आयत के क्षेत्रफल का आधा है। दर्शाइए कि, P का बिन्दुपथ एक दीर्घवृत्त होगा, जिसकी उत्केन्द्रता √23 होगी तथा यह BAC से गुजरता है।
View Solution