In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
locus of P is an ellipse with eccentricity √23
locus of P is a hyperbola with eccentricity √32
area of the quadr5ilateral ABCD=163 sq. units
area of the quadrilateral ABCD=323 sq. units
The correct Answer is:A, C
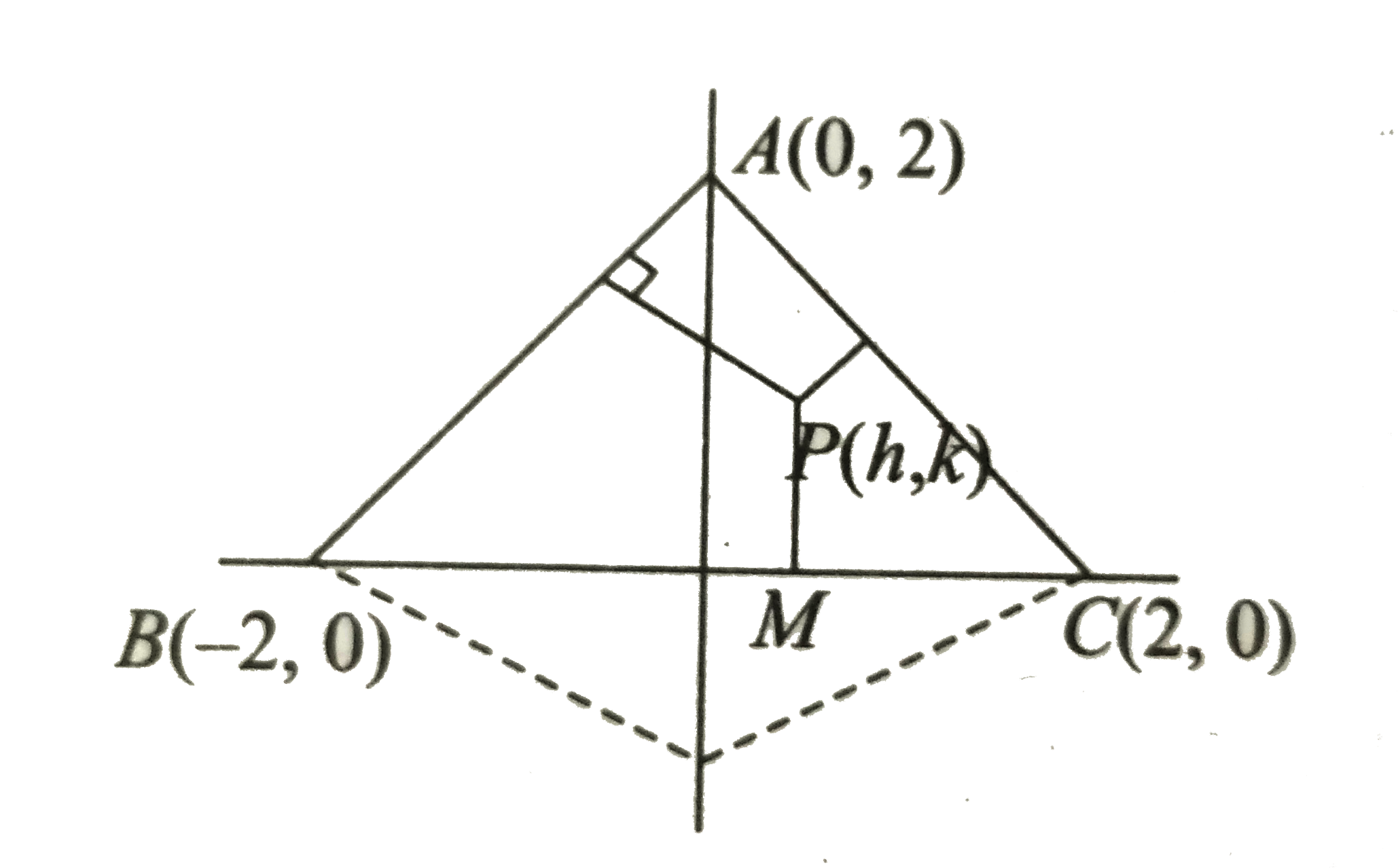
PM=k
Equation of AB≡x+y=2
Equation of AC≡x+y=2
According to question
(2−h−k√2)(2+h+k√2)=2k2
⇒h2+3k2+4k=4
⇒h2+3(k2+43k+49)=4+43
⇒h2+3(k+23)2=163⇒h216/3+(k+23)216/9=1
⇒ Ellipse with e=√23 and D≡(0,−23).
Topper's Solved these Questions
Similar Questions
ABC is an isosceles triangle with its base BC twice its altitude. A polnt P moves within the triangle such that the square of its distance from BC is half the rectangle contained by its distances from the two sides. Show that the locus of P is an ellipse with eccentricity √23 passing through B&C.
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:
View Solution
Knowledge Check
The locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
AcircleBstraight lineCellipseDnoneLocus of a point which moves such that sum of the squares of its distances from the sides of a square of side unity is 9, is
Astraight lineBcircleCparabolaDnoneIn a triangle ABC, AB = 5 , BC = 7, AC = 6. A point P is in the plane such that it is at distance '2' units from AB and 3 units form AC then its distance from BC
Ais 12√6−287 when P is inside the trinagleBmay be 12√6−87 when P is outside the triangleCmay be 12√6+147 when P is inside the triangleDmay be 12√6+147 when P is outside the triangle
A point p is such that the sum of squares of its distance from the axes of coordinates is equal to the square of its distance from the line x−y=1. Find the locus of P
View SolutionA point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point
View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionA point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point is
View SolutionThe locus of a point which moves such that the sum of the squares of the distances from the three vertices of a triangle is constant, is a circle whose centre is at the:
View Solution