The straight line x4+y3=1 intersects the ellipse x216+y29=1 at two points A and B, there is a point P on this ellipse such that the area of ΔPAB is equal to 6(√2−1). Then the number of such points (P) is/are Solution in Tamil
0
1
2
3
The correct Answer is:D
Let the perpendicular distance of P from the line be h,
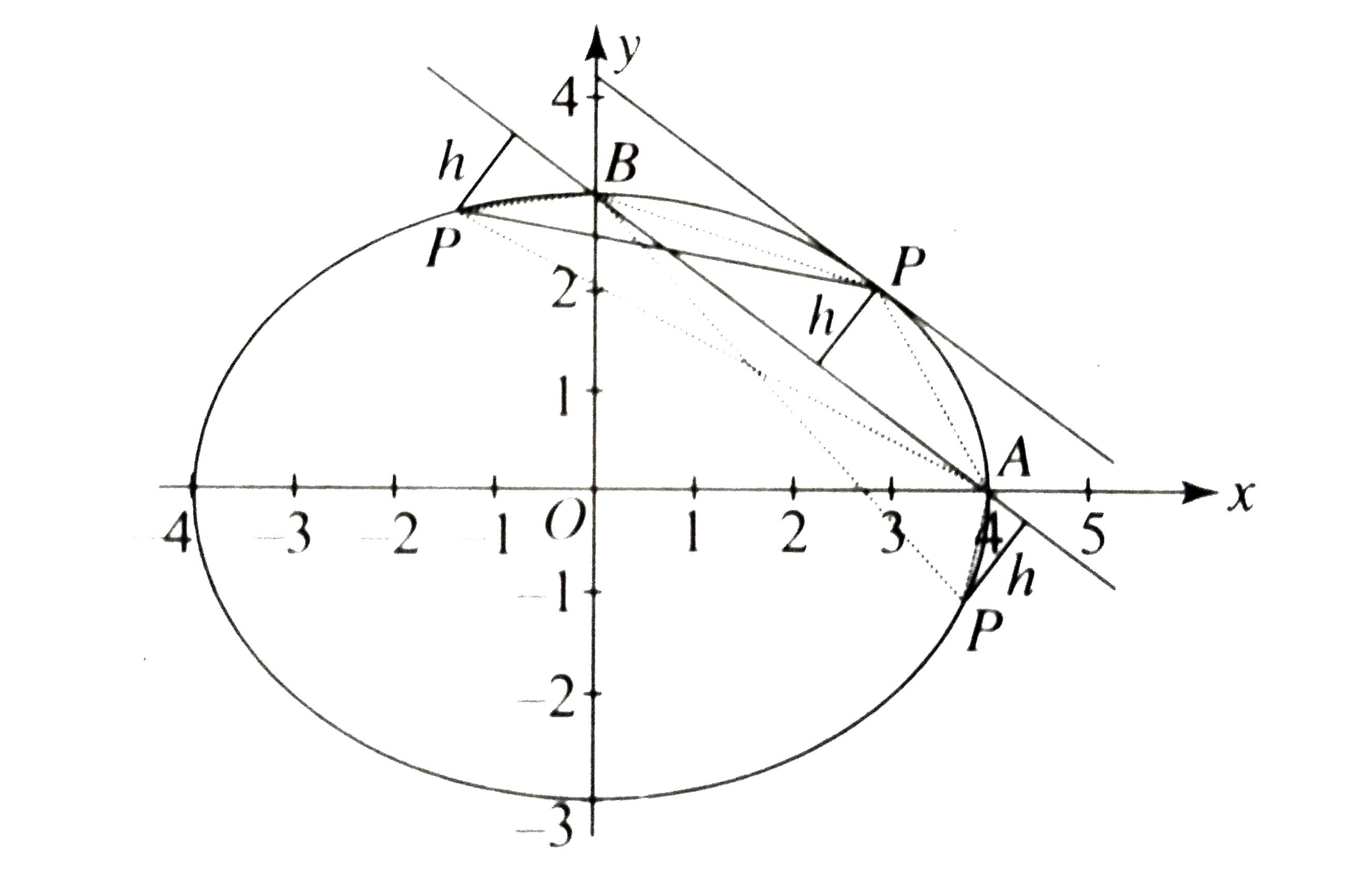
∴12×h×5=6(√2−1)
∴h=125(√2−1)
Also tangent parallel to the given line is 4y+3x=12√2
Its distance from the line 4y+3x=12 is h=125(√2−1) Hence there are three points as shown in the figure.
Topper's Solved these Questions
Similar Questions
In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
View SolutionLet a,b>0 and →α=(→ia+4ˆjb+bˆk) and →β=bˆi+aˆj+1bˆk, then the maximum value of 305+→α.→β is
View SolutionLet any double ordinate PNP' of the hyperbola x225−y216=1 be produced on both sides to meet the asymptotes in QandQ' . Then PQ.P′Q is equal to 25 (b) 16 (c) 41 (d) none of these
View SolutionTangents are drawn from the point P(3,4) to the ellipse (x^(2))/(9)+(y^(2))/(4)=1 touching the ellipse at points A and B.
View SolutionThe straight line (x)/(4)+(y)/(3)=1 intersects the ellipse (x^(2))/(16)+(y^(2))/(9)=1 at two points A and B such that area of Delta PAB is equal to 3, the number of such P's is/are
View SolutionThe straight line x4+y3=1 intersects the ellipse x216+y29=1 at two points A and B there is a point P on this ellipse such that the area of ΔPAB is equal to 6(√2−1) .Then the number of such point (P) is/are
View SolutionThe straight line x4+y3=1 intersects the ellipse x216+y29=1 at two points A and B there is a point P on this ellipse such that the area of Delta PAB is equal to 6(√2−1) . Then the number of such point (P) is/are (A) 4 (B) 1 (C) 2 (D) 3
View SolutionThe locus of the point of intersection of perpendicular tangents to the ellipse (x−1)216+(y−2)29=1 is
View SolutionIf the line y=x+sqrt(3) touches the ellipse (x^(2))/(4)+(y^(2))/(1)=1 then the point of contact is
View SolutionThe locus of point intersection of perpendicular tangents of ellipse ((x-1)^(2))/(16)+((y-1)^(2))/(9)=1 is
View SolutionIf ellipses (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 The tangent lines drawn at P intersect perpendicular to P, then the point p of P x^(2)+y^(2)=a^(2)+b^(2) is. This circle is called
View SolutionList−IList−IIThe number of rational points on the ellipsex29+y24=14The number of integral points on the ellipsex29+y24=12The number of integral points on the ellipsex23+y21=1∞
View SolutionThe straight line x4+y3=1 intersects the ellipse x216+y29=1 at two points A and B, there is a point P on this ellipse such that the area of ΔPAB is equal to 6(√2−1). Then the number of such points (P) is/are
View SolutionThe line y=2t2 intersects the ellipse x29+y24=1 in real points if
View Solutionबिन्दु P(3, 4) से दीर्घवृत्त x29+y24=1 पर खींची गई स्पर्श रेखाएं इस दीर्घवृत्त को A एवं B बिन्दुओं पर स्पर्श करती है।
उस बिन्दु के बिन्दुपथ का समीकरण, जिसकी बिन्दु P तथा सरल रेखा AB से दूरियाँ बराबर हैं, होगा
View Solution
