An ellipse passes through the point (2,3) and its axes along the coordinate axes, 3x+2y−1=0 is a tangent to the ellipse, then the equation of the ellipse is Solution in Tamil
x24+4y2=1
x28+y21=1
4x2+y24=1
No such ellipse exists
The correct Answer is:D
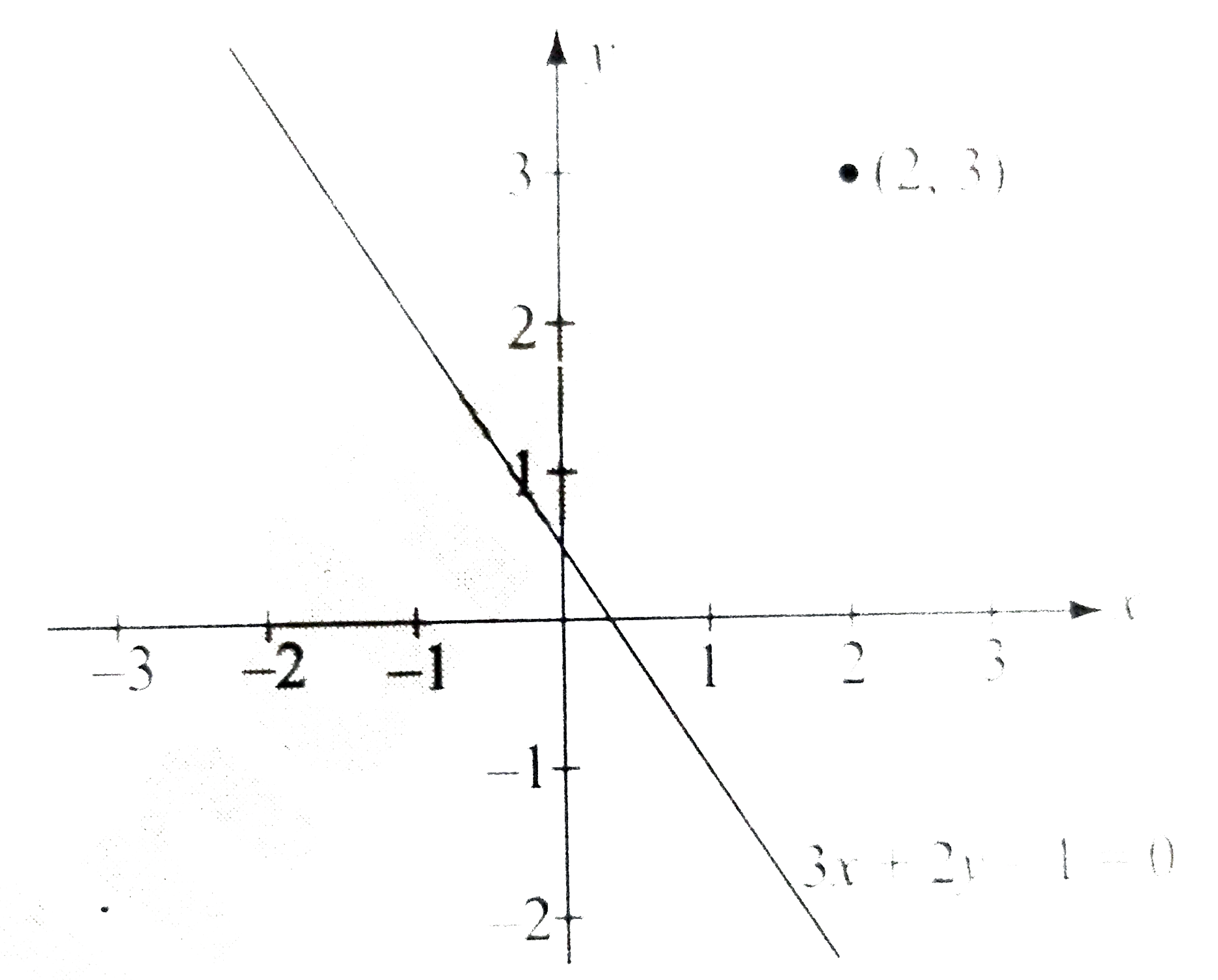
From the position of line and point, it is clear that no such ellipse exists.
Topper's Solved these Questions
Similar Questions
In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
View SolutionLet a,b>0 and →α=(→ia+4ˆjb+bˆk) and →β=bˆi+aˆj+1bˆk, then the maximum value of 305+→α.→β is
View SolutionLet any double ordinate PNP' of the hyperbola x225−y216=1 be produced on both sides to meet the asymptotes in QandQ' . Then PQ.P′Q is equal to 25 (b) 16 (c) 41 (d) none of these
View SolutionAn ellipse passes through the point (4,−1) and touches the line x+4y−10=0 . Find its equation if its axes coincide with the coordinate axes.
View SolutionAn ellipse passes through the points (-3,1)&(2,-2)& its principal axis are along the coordinate axes in order.Find its equation.
View SolutionAn ellipse passes through the point (2,3) and its axes along the coordinate axes, 3x+2y−1=0 is a tangent to the ellipse, then the equation of the ellipse is
View SolutionIf the major and minor axes of the ellipse are the axes of coordinates, then the equation of the ellipse passing through the points (2,−2)and(−3,1) is-
View SolutionThe equation of the ellipse refered to its axes as coordinate axes, which passes through the points (2, 2) and (1, 4) is
View SolutionThe equation of the ellipse referred to its axes as coordinate axes, which passes through the point (2, 2) and (1, 4) is
View SolutionAn ellipse passes through the point (4,−1) and touches the line x+4y−10=0 . Find its equation if its axes coincide with the coordinate axes.
View SolutionAn ellipse passes through the point (2,3) and its axes along the coordinate axes, 3x+2y−1=0 is a tangent to the ellipse, then the equation of the ellipse is
View SolutionIf the foci of an ellipse are (0,±1) and the minor axis is of unit length, then find the equation of the ellipse. The axes of ellipse are the coordinate axes.
View Solutionउस दीर्घवृत्त का समीकरण, जिसके अक्ष निर्देशांक अक्षों के अक्ष हैं तथा जो बिन्दु(-3, 1) से गुजरता है तथा उत्केन्द्रता √25 है, होगा
View SolutionAn ellipse intersects the hyperbola 2x2−2y2=1 orthogonally. The eccentricity of the ellipse is reciprocal of that of the hyperbola. If the axes of the ellipse are along the coordinate axes, then
View SolutionIf the foci of an ellipse are (0,±1) and the minor axis is of unit length, then find the equation of the ellipse. The axes of ellipse are the coordinate axes.
View Solution
