Draw the graph of $f (x) = \log_{e} (\sqrt{1 - x^{2}} - x)$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

We have $y = f (x) = \log_{e} (\sqrt{1 - x^{2} - x})$
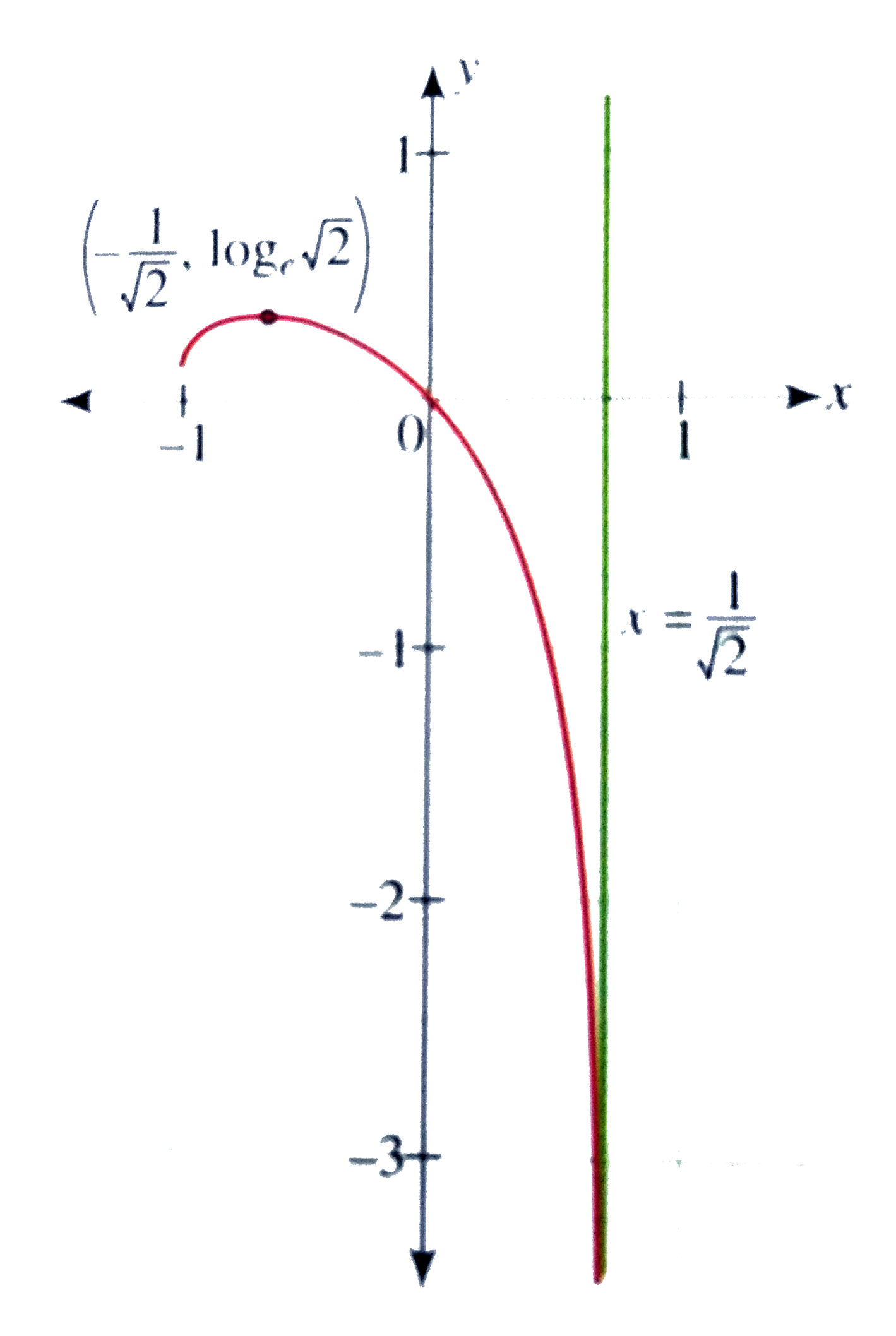
$f (x)$ is defined if $\sqrt{1 - x^{2}} - x > 0$ and $1 - x^{2} \geq 0$
For $1 - x^{2} \geq 0, - 1 \leq x \leq 1$
$\sqrt{1 - x^{2}} - x > 0$
For (0,1),
$1 - x^{2} > x^{2}$
or $0 < x < \frac{1}{\sqrt{2}}$
Thus, the domain of the function is $[- 1, \frac{1}{\sqrt{2}}]$
$f^{'} (x) = \frac{(- \frac{x}{\sqrt{1 - x^{2}}}) - 1}{\sqrt{1 - x^{2}} - x}$
$= \frac{- x - \sqrt{1 - x^{2}}}{(\sqrt{1 - x^{2}} \sqrt{1 - x^{2}} - x)}$
$f^{'} (x) = 0 ∴ - x = \sqrt{1 - x^{2}}$
$∴ x = - \frac{1}{\sqrt{2}}$
$f^{'} (x) > 0$ for $x \in (- 1, - \frac{1}{\sqrt{2}})$
$f^{'} (x) < 0$ for $x \in (- \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$
So $x = - \frac{1}{\sqrt{2}}$ is the point of maxima.
$f (- 1) = f (0) = 0$
$lim_{x \to \frac{1}{\sqrt{2}}} \log_{e} (\sqrt{1 - x^{2}} - x) = - \infty (∴ lim_{x \to \frac{1}{\sqrt{2}}} (\sqrt{1 - x^{2}} - x) = 0)$
Thus, $x = \frac{1}{\sqrt{2}}$ is an asymptote.
From the above discussion, the graph of the function is as shows in the following figure.

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

CENGAGE-CURVE TRACING-Exercise

Home
Ask Doubt
Profile