If the area of the region is , then the value of is____Solution in Tamil
The correct Answer is:6
Draw the given region point of intersection of
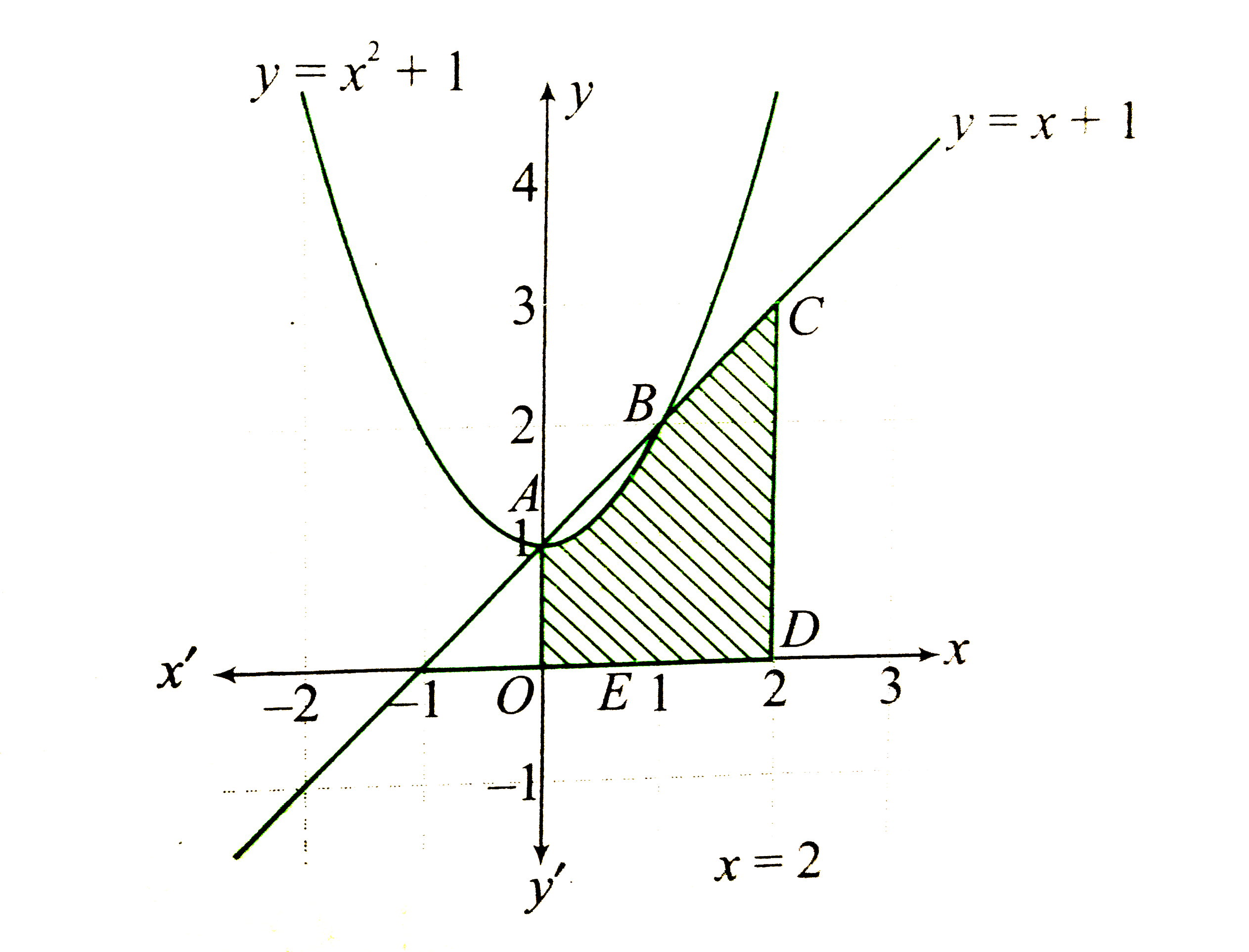
sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0.
View SolutionMatch the following lists :

View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIf the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2} is A , then the value of 3A−17 is____
View SolutionSolve each of the following linear programming problems by graphical method. Maximize Z=x+y Subject to −2x+y≤1 x≤2 x+y≤3 x,y≥0
View SolutionThe absolute value of |x−2|+|x+2|, if 0<x<2 is
View SolutionFind the area bounded by the curve x=⎧⎪⎨⎪⎩−2−y,y<−1y3,−1≤y≤12−y,y>1 and x=0 is
View SolutionFind the area of the region {(x,y):x2<y<x}
View SolutionIf s∈−1x=y, then (A) 0≤y≤π (B) −π2≤y≤π2(C) 0<y<π (d) −π2<y<π2
View SolutionUsing integration, find the area of the following region : {(x,y); |x+2|≤y≤√20−x2}
View SolutionIf m is the minimum value of f(x,y)=x2−4x+y2+6y when xandy are subjected to the restrictions 0≤x≤1and0≤y≤1, then the value of |m| is________
View SolutionIf the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2} is A , then the value of 3A−17 is____
View SolutionFind the area bounded by the curve x=⎧⎪⎨⎪⎩−2−y,y<−1y3,−1≤y≤12−y,y>1 and x=0 is
View SolutionFind the area of the region {(x,y):x2≤y≤|x|}.
View Solution
