Consider the sequence of natural numbers s0,s1,s2,... such that s0=3,s1=3andsn=3+sn−1sn−2, thenSolution in Tamil
eπ2
e−π
eπ
e−π2
The correct Answer is:C
Since −1≤sinx≤1, the curve y=e−xsinx is bounded by the curve y=e−xandy=e−x.
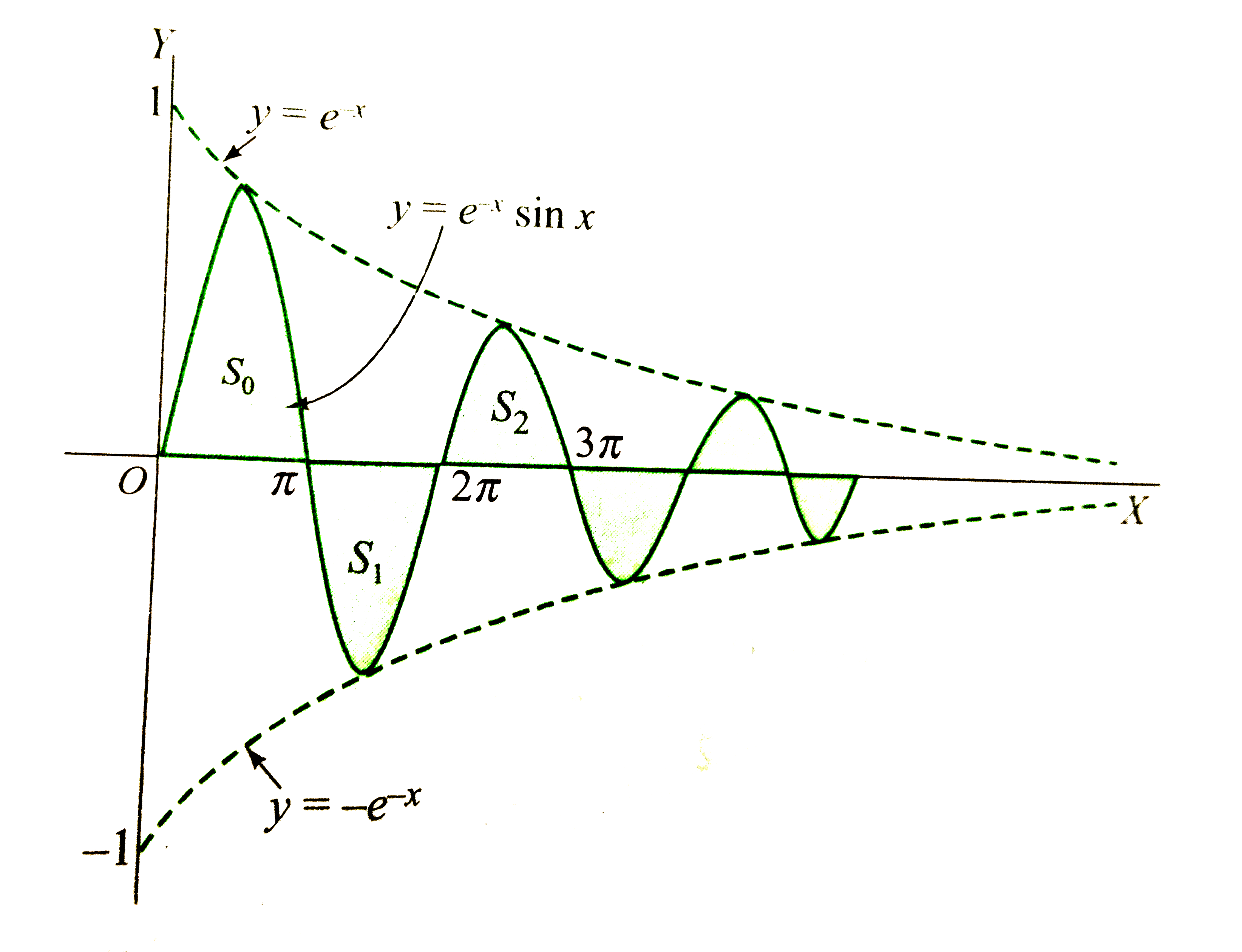
Also, the curve y=e−xsinx intersects the positive semi-axis OX at the points where sin x=0, where xn=nπ,n∈Z.
Also |yn|=|y coordinate in the half-wave Sn|
∴ Sn=(−1)n(n+1)π∫nπe−xsinxdx
=(−1)n+12[e−x(−sinx+cosx)](n+1)πnπ
=(−1)n+12[e−(n+1)x(−1)n+1−enπ(−1)n]
=e−nπ2(1+eπ)
⇒ Sn+1Sn=e−π
and S0=12(1+eπ).
Therefore, the sequence S0,S1,S2,... forms an infinite G.P. with common ratio e−π. we have
∞Σn=0Sn=12(1+eπ)1−e−π
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Match the following lists :

View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIf S_1,S_2,S_3,...,S_n be the sums of first n terms of n G.P.'s whose first terms are each unity and the common ratios are 1, 2, 3,.....,n respectively, prove that S_1+S_2+2S_3+3S_4+.........+(n-1)S_n=1^n+2^n+3^n+....+n^n.
View SolutionConsider the sequence of natural numbers s_(0),s_(1),s_(2),... such that s_(0)=3,s_(1)=3 and s_(n)=3+s_(n-1)s_(n-2) then
View SolutionIf sum of n terms of a sequence is Sn then its nth term tn=Sn−Sn−1. This relation is valid for all n>−1 provided S0=0. But if S1=0, then the relation is valid only for n≥2 and in hat cast t1 can be obtained by the relationt1=S1. Also if nth term of a sequence t1=Sn−Sn−1 then sum of n term of the sequence can be obtained by putting n=1,2,3,.n and adding them. Thus n∑n=1tn=Sn−S0. if S0=0,thenn∑n=1tn=Sn. On the basis of above information answer the following questions: If the sum of n terms of a sequence is 10n2+7n then the sequence is (A) an A.P. having common difference 20 (B) an A.P. having common difference 7 (C) an A.P. having common difference 27 (D) not an A.P.
View Solutionयदि किसी समान्तर श्रेढ़ी के n पदों का योग Sn हो तथा S1=6, और S7=105, तो सिद्ध कीजिए की Sn:Sn−3=(n+3):(n−3) .
View SolutionLet Sn=cos(nπ10),n=1,2,3,…… then the value of s1s2……s10s1+s2+……..+s10 is equal to
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
The last element in the S24 is :
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
The middlemost element of the set S15 is:
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
The sum of the elements of set S25 is :
View SolutionFor any natural number n the sets S1,S2,….. are defined as below:
S1={1}.S2={2,3},S3={4,5,6}
S4={7,8,9,10},S5={11,12,13,14,15}: etc.
On which set the sum of all the elements of the set is even :
View SolutionIf S1,S2,S3 are the sum of first n natural numbers, their squares and their cubes, respectively , show that 9S22=S3(1+8S1)
View SolutionIf S1,S2,S3 are the sum of first n natural numbers, their squares and their cubes, respectively , show that 9S22=S3(1+8S1)
View Solution
