Consider the sequence of natural numbers s0,s1,s2,... such that s0=3,s1=3andsn=3+sn−1sn−2, then
eπ2
e−π
eπ
e−π2
The correct Answer is:C
Since −1≤sinx≤1, the curve y=e−xsinx is bounded by the curve y=e−xandy=e−x.
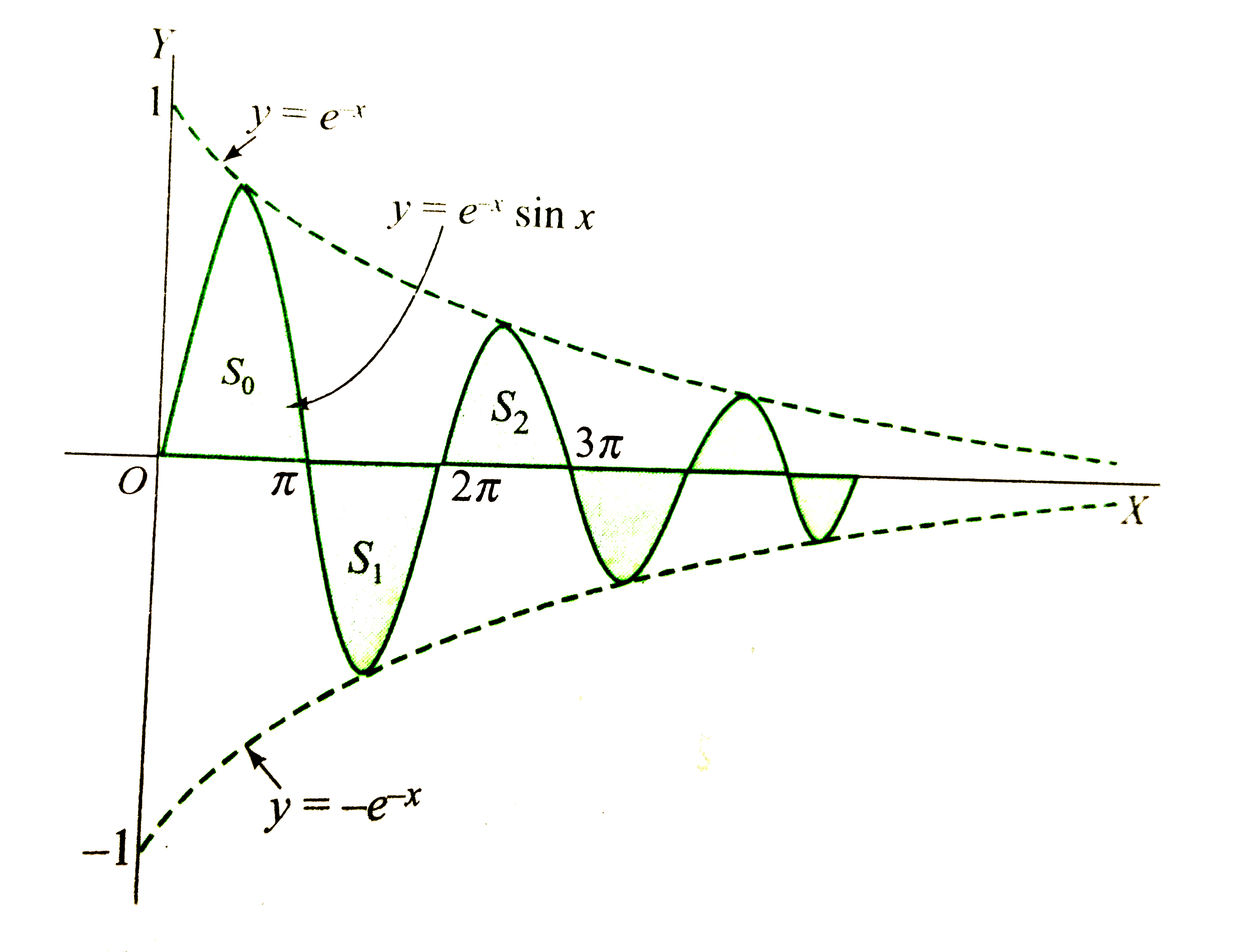
Also, the curve y=e−xsinx intersects the positive semi-axis OX at the points where sin x=0, where xn=nπ,n∈Z.
Also |yn|=|y coordinate in the half-wave Sn|
∴ Sn=(−1)n(n+1)π∫nπe−xsinxdx
=(−1)n+12[e−x(−sinx+cosx)](n+1)πnπ
=(−1)n+12[e−(n+1)x(−1)n+1−enπ(−1)n]
=e−nπ2(1+eπ)
⇒ Sn+1Sn=e−π
and S0=12(1+eπ).
Therefore, the sequence S0,S1,S2,... forms an infinite G.P. with common ratio e−π. we have
∞Σn=0Sn=12(1+eπ)1−e−π
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Knowledge Check
A sequence is defined for all positive integers by sn=2sn−1+n+1 and s1=3. What is s4?
A9B18C22D49Let Sn denote the sum of the cubes of the first n natural numbers and sn denote the sum of first n natural numbers then Snsn is equal to
(i) n(n+1)(n+2)6
(ii) n(n+1)2
(iii) n2+3n+22
(iv) 2n+13An(n+1)(n+2)6Bn(n+1)2Cn2+3n+22D2n+13
Let Sn denote the sum of the cubes of the first n natural numbers and sn denote the sum of the first n natural numbers. Then n∑r=1Srsr is equal to
View SolutionIf Sn, be the sum of n terms of an A.P; the value of Sn−2Sn−1+Sn−2, is
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2and S3, respectively, show that S3=3(S2−S1).
View SolutionIf S1,S2,S3 are the sums of first n natural numbers, their squares and cubes respectively, show that 9S22=S3(1+8S1).
View SolutionIf sum of n termsof a sequende is Sn then its nth term tn=Sn−Sn−1. This relation is vale for all n>−1 provided S0=0. But if S≠0, then the relation is valid ony for n≥2 and in hat cast t1 can be obtained by the relationt1=S1. Also if nth term of a sequence t1=Sn−Sn−1 then sum of n term of the sequence can be obtained by putting n=1,2,3,.n and adding them. Thus n∑n=1tn=Sn−S0. if S0=0,thenn∑n=1tn=Sn. On the basis of above information answer thefollowing questions:If nth term of a sequence is n1+n2+n4 then the sum of its first n terms is (A) n2+n1+n+n2 (B) n2−n1+n+n2 (C) n2+n1−n+n2 (D) n2+n2(1+n+n2)
View SolutionIf sum of n terms of a sequence is Sn then its nth term tn=Sn−Sn−1. This relation is valid for all n>−1 provided S0=0. But if S1=0, then the relation is valid ony for n≥2 and in that case t1 can be obtained by the relationt1=S1. Also if nth term of a sequence tn=Sn−Sn−1 then sum of n term of the sequence can be obtained by putting n=1,2,3,.n and adding them. Thus n∑n=1tn=Sn−S0. if S0=0,thenn∑n=1tn=Sn. On the basis of above information answer thefollowing questions: If nth term of a sequence is 1(n+2)n! then sum of to infinity of this sequence is (A) 1 (B) 12 (C) 13 (D) none of these
View Solution
