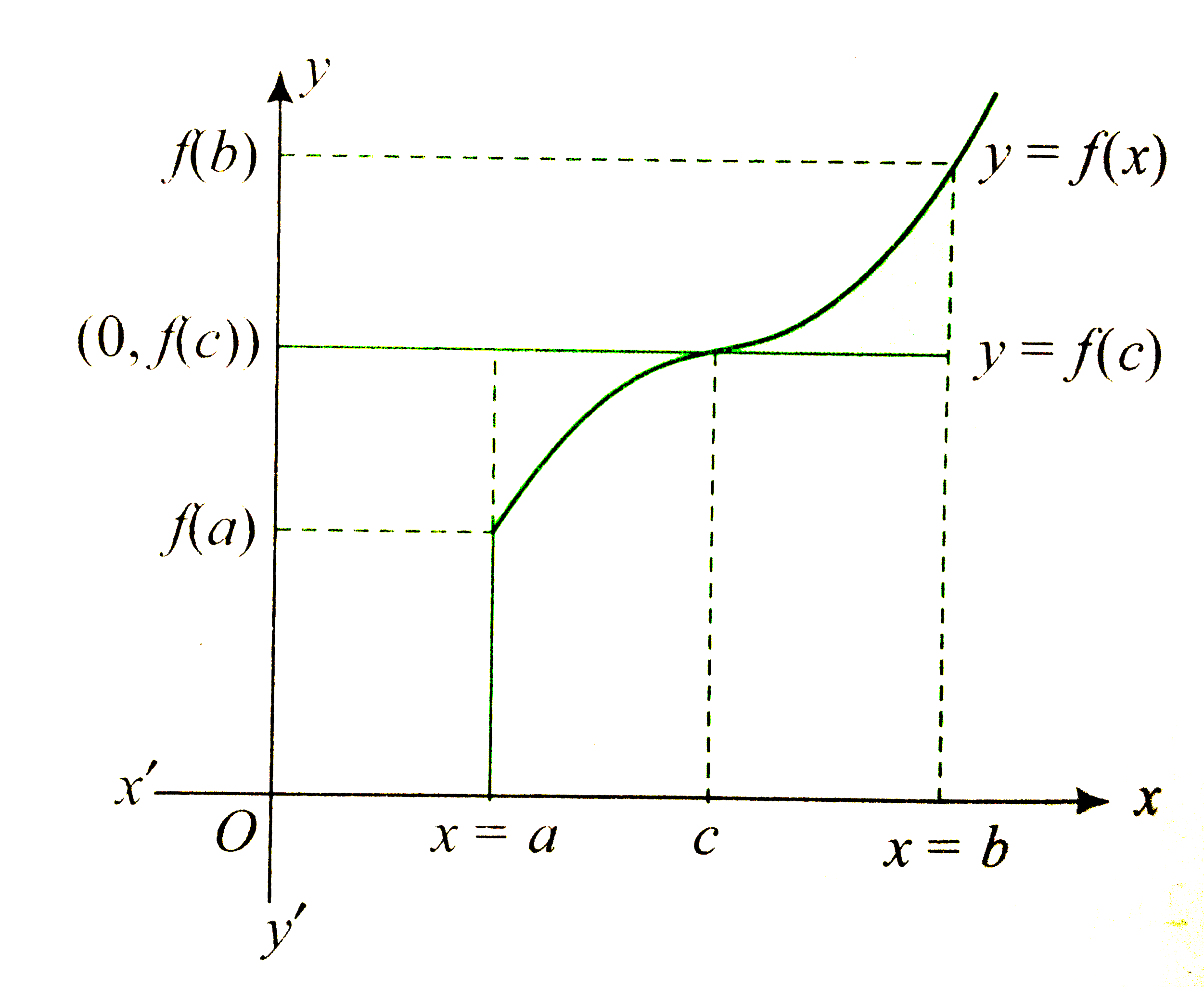
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is
0
-1
1
2
The correct Answer is:A
f(x)=sinx+cosx
or df(x)dx=cosx−sinx
If df(x)dx=0, then cosx=sinx⇒x=π4andx=5π4
(considering any two of consecutive points of extremum).
For minimum area bounded by y=f(x)andy=a, between
x=π4andx=5π4, graphs of g(x) must cut y =a at
c=π4+5π42=3π4.
a=f(3π4)
⇒ a=sin(3π4)+cos(3π4)=0.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type18videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type13videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
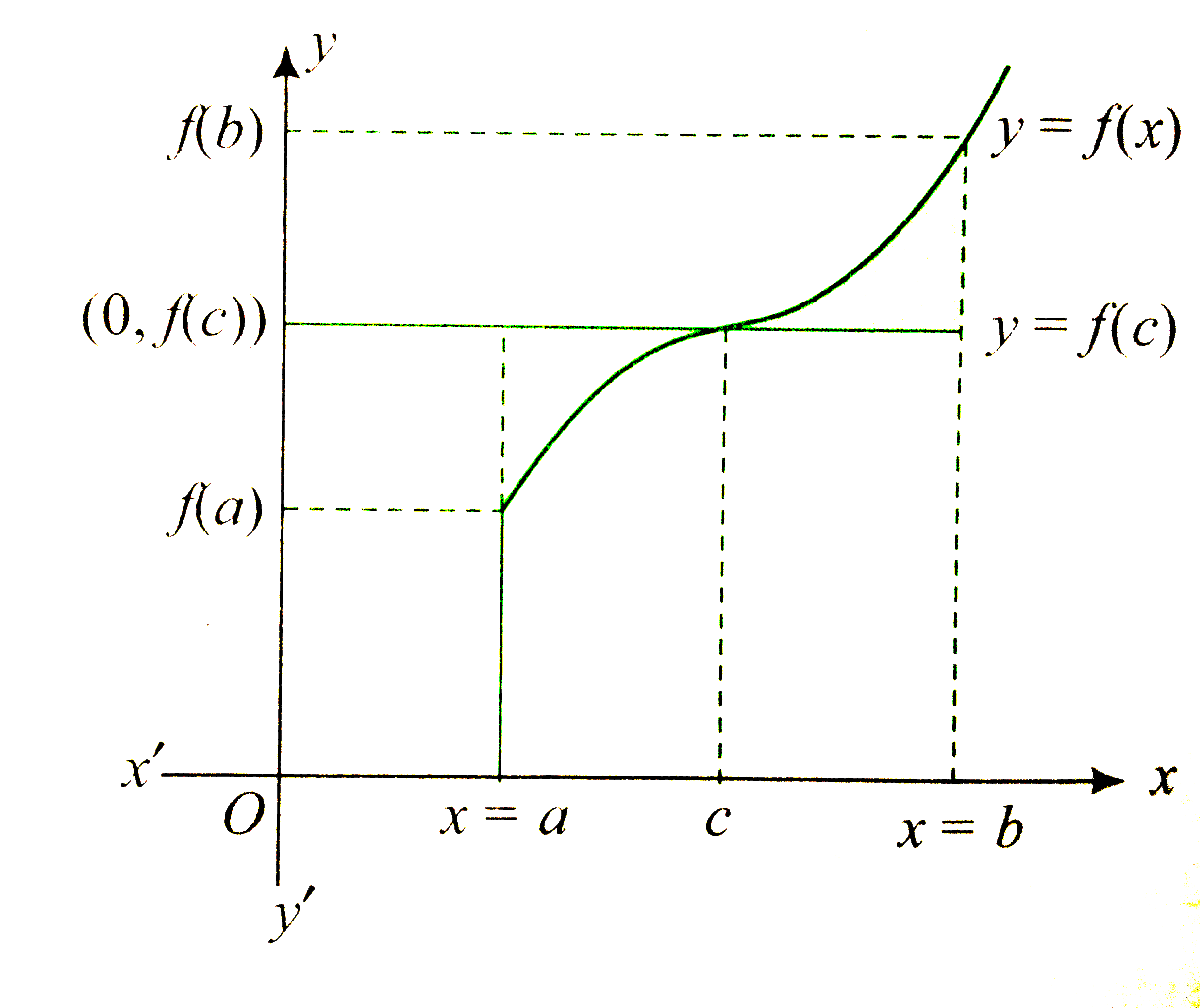
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
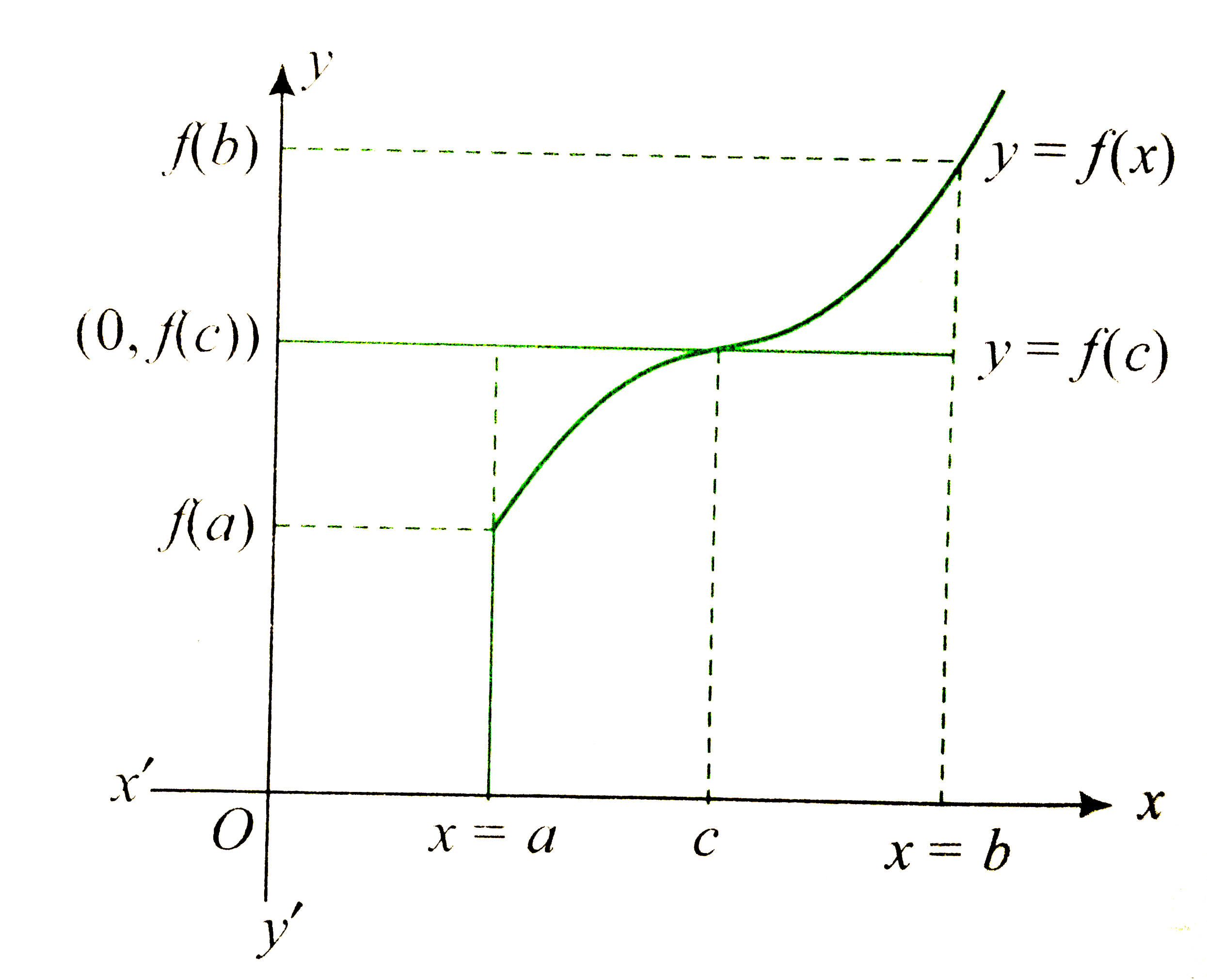
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a isView SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b))isminiμmwhen
c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, isView Solution
Knowledge Check
- Question 1 - Select One
∫b+ca+cf(x)dx is equal to
A∫baf(x−c)dxB∫baf(x+c)dxC∫baf(x)dxD∫b−ca−cf(x)dx
1c∫bcacf(xc)dx=
View SolutionIf ∣∣∣∫baf(x)dx∣∣∣=∫ba|f(x)|dx,a<b,then f(x)=0 has
View SolutionLet ∫baf(x)dx=∫b+ca+cf(x−c)dx. Then the value of ∫π0sin2010x⋅cos2009xdx is
View SolutionProve that ∫baf(x)dx=∫b+ca+cf(x−c)dx , and when f(x) is odd function, ∫a−af(x)dx=0
View SolutionWhich of the following is incorrect? ∫b+ca+cf(x)dx=∫baf(x+c)dx ∫bcacf(x)dx=c∫baf(cx)dx ∫a−af(x)dx=12∫a−a(f(x)+f(−x)dx None of these
View Solution∫a0[f(x)+f(−x)]dx= (A) 0 (B) 2∫a0f(x)dx (C) ∫a−af(x)dx (D) none of these
View SolutionSTATEMENT-1 : ∫5π−2πcot−1(tanx)dx=7π22
and
STATEMENT-2 : ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx, a<c<bView Solution
