Compute the area of the region bounded by the curves y=ex(logex)andy=logexexSolution in Tamil
The given curves are
y=exlogex (1)
y=logxex (2)
The two curves intersect where exlogx=logxex
⇒ (ex−1ex)logx=0⇒x=1eorx=1
At x=1/e,y=−1(from(1))
At x=1,y=0(from(1))
So points of intersection are (1e,−1)and(1,0).

From the above information, the rough sketch of two curves is as shown in the figure and the shaded area is the required area.
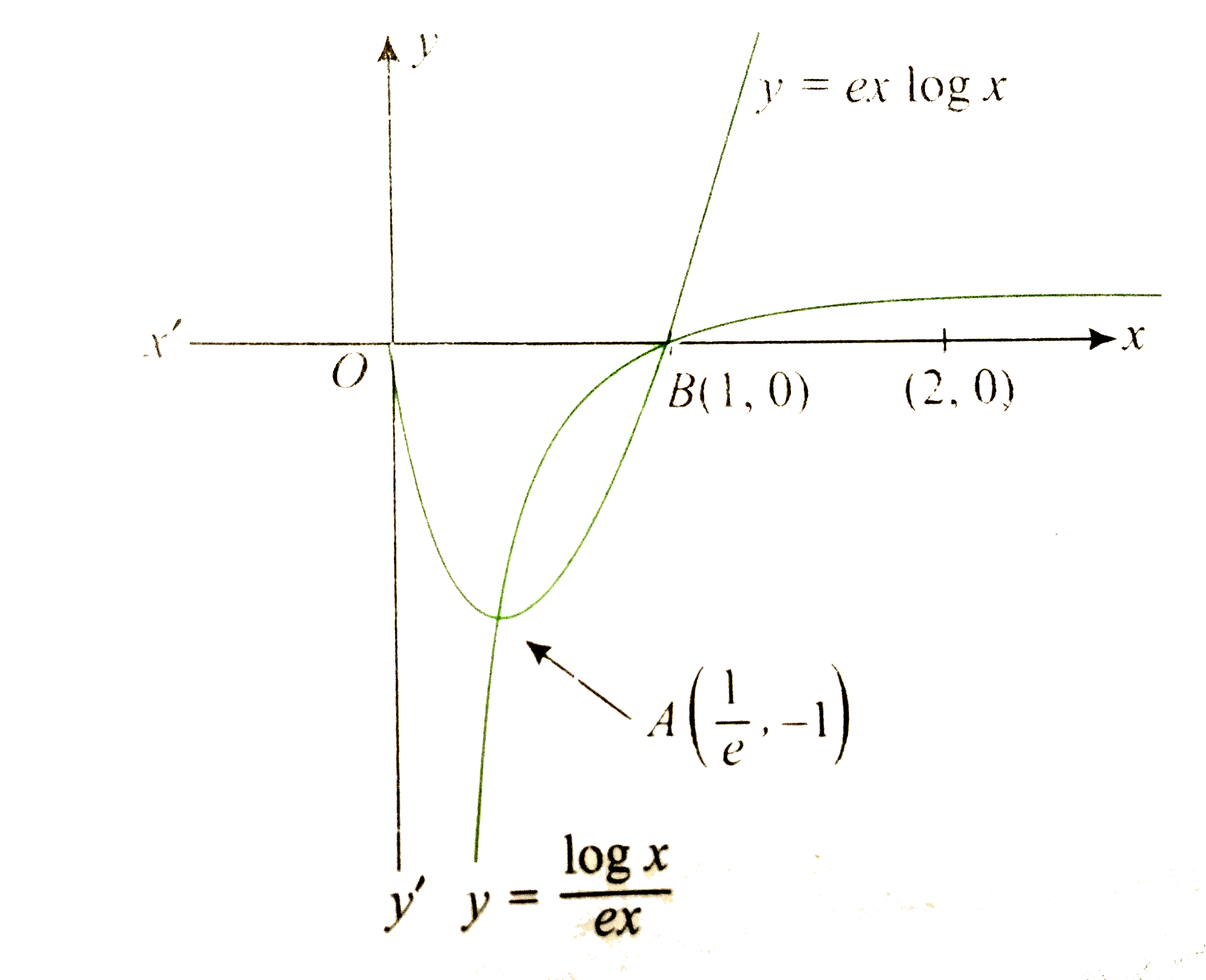
∴ Required area = Area of the shaded region
=∣∣∣∫11/e[exlogx−logxex]dx∣∣∣
=∣∣
∣∣e[x22logx−x24]11/e−1e[(logx)2]11/e∣∣
∣∣
=∣∣∣e[(−14)−(−12e2−14e2)]−1e[0−12]∣∣∣
∣∣∣e[−14+34e3]+12e∣∣∣
=∣∣∣5−e24e∣∣∣=e2−54e sq. units.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
05:31View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
02:22View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
06:06View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the area bounded by y=logex,y=−logex,y=loge(−x),andy=−loge(−x).
02:12View SolutionThe area bounded by the curve y=2^(x), the x- axis and the left of y-axis is (A) log _(e)2(B)log_(e)4 (C) log_(4)e(D)log_(2)e
04:17View SolutionSketch the region bounded by the curves y=log_(e)x and y=(log_(e)x)^(2). Also find the area of the region.
04:51View SolutionDraw the graph of y=loge(−x),−logex,y=|logex|,y=loge|x| and y=|loge|x|| transforming the graph of y=logex.
View SolutionThe area (in sq units) of the region bounded by the curves y=ex, y=loge x and lines x = 1, x = 2 is
11:01View SolutionThe area bounded by the curve y=logex, the x-axis and the straight line x=e
03:08View Solutionवक्र y=logex, X-अक्ष तथा कोटियों x = 1 तथा x = e से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
04:23View Solutionवक्रों y=exlogex और y=logexex घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।( दिया है: logee=1)
01:58View SolutionFind the area of the region bounded by the curves, y=logex,y=sin4πxandx=0.
06:39View SolutionArea bounded by the curves y=ex,y=logex and the lines x=0,y=0,y=1 is
05:39View Solutionवक्र y=logex तथा निर्देशांक अक्षो द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
07:21View SolutionArea bounded by the curve y=logex,x=0,y≤0 and x-axis is:
05:12View Solution
