Find the area bounded by y=−x3+x2+16xandy=4xSolution in Tamil
Solving given curve, we have
−x3+x2+16x=4x
∴ x=0orx2−x−12=0
⇒ x=0or(x−4)(x+3)=0
⇒ x=0orx=−3,4
Now y=−x3+x2+16
=−x(x2−x−16)
If y=0 then x=0orx2−x−16=0
∴ x=0orx1±√652
From the above in information we having following graphs.
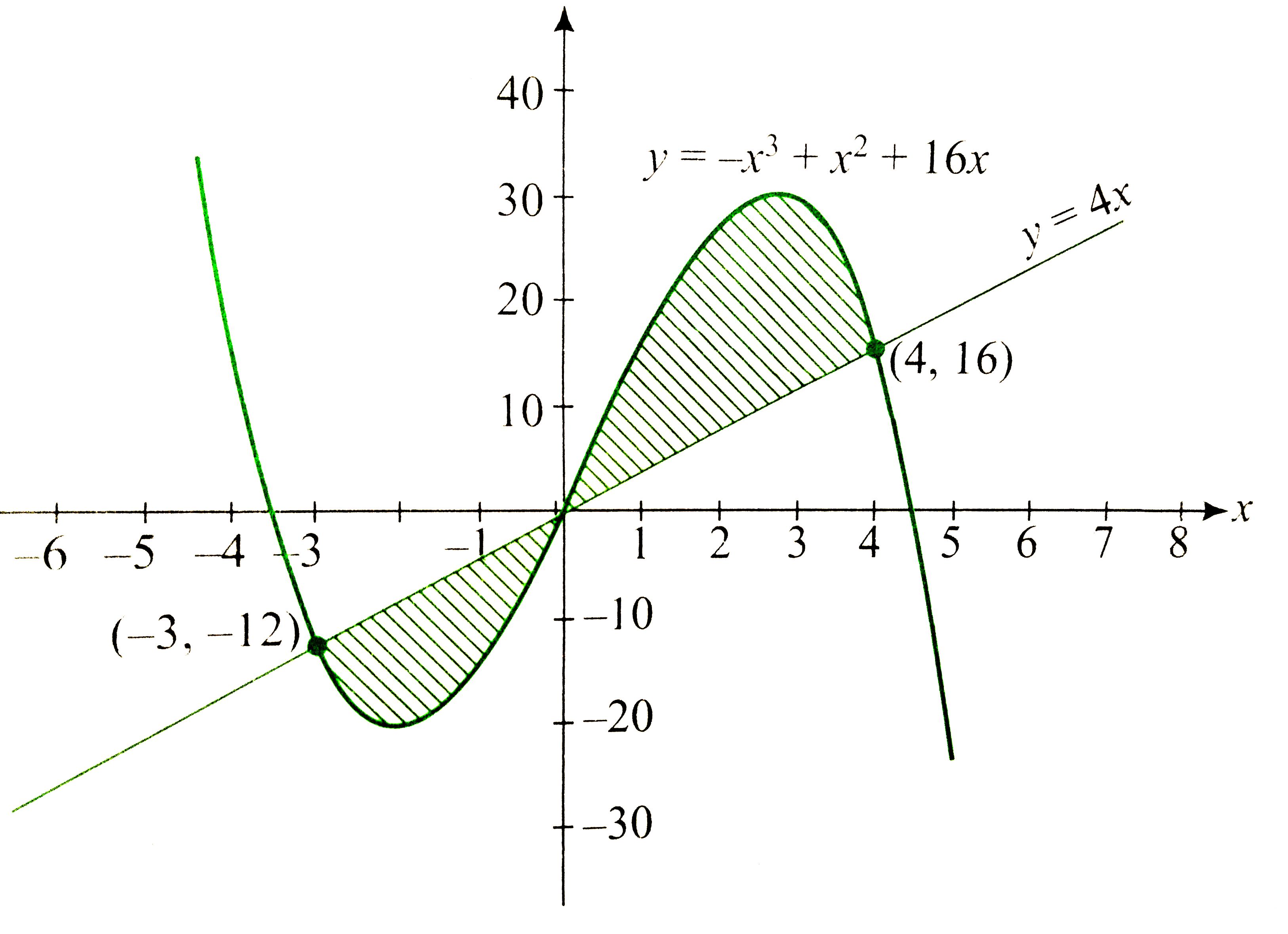
From the figure area of the shaded region,
A=0∫−3[4x−(−x3+x2+16x)]dx+4∫0[(−x3+x2+16x)−4x]dx
=0∫−3(x3−x2−12x)dx+4∫0(−x2+x2+12x)dx
=[x44−x33−6x2]0−3+[−x44+x33+6x2]40
=[−814−9+54]+[−64+643+96]
=93712 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionThe area bounded by the x-axis and the curve y=4x−x2−3 is
View SolutionFind the area bounded by y=−x3+x2+16xandy=4x
View SolutionFind the area of the region if the first quadrant bounded by the parabola y2=4x, the line x+y=3 and y-axis.
View SolutionFind the area of the region bounded by the parabolas y2=4xandx2=4y
View SolutionThe area bounded by the X-axis and the curve y=4x−x2−3 is
View SolutionFind the area bounded by the curves x2=y, x2=−y and y2=4x−3
View SolutionFind the area bounded by y=−x3+x2+16xandy=4x
View SolutionFind the area bounded by the parabolas : y2=16x and x2=16y.
View SolutionFind the area of the region bounded by
y=x2andy=x3
View Solutionfind the area of the region bounded by 'y^2=4x' and x=2
View SolutionThe area bounded by x-axis and the curve y=4x−x2−3 is
View Solution
