Suppose that f(x) is a function of the form f(x) =ax8+bx6+cx4+dx2+15x+1x,(x≠0).Iff(5)= -28thenthevalueoff(-5)/14 is____Solution in Tamil
The correct Answer is:28
f(x)=ax8+bx6+cx4+dx2+15x+1x
=ax7+bx5+cx3+dx+1x+15odd function
Now, f(x)+f(−x)=30
orf(−5)=30−f(5)=28
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year
12 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
For real x, let f(x)=x3+5x+1 , then (1) f is oneone but not onto R (2) f is onto R but not oneone (3) f is oneone and onto R (4) f is neither oneone nor onto R
View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
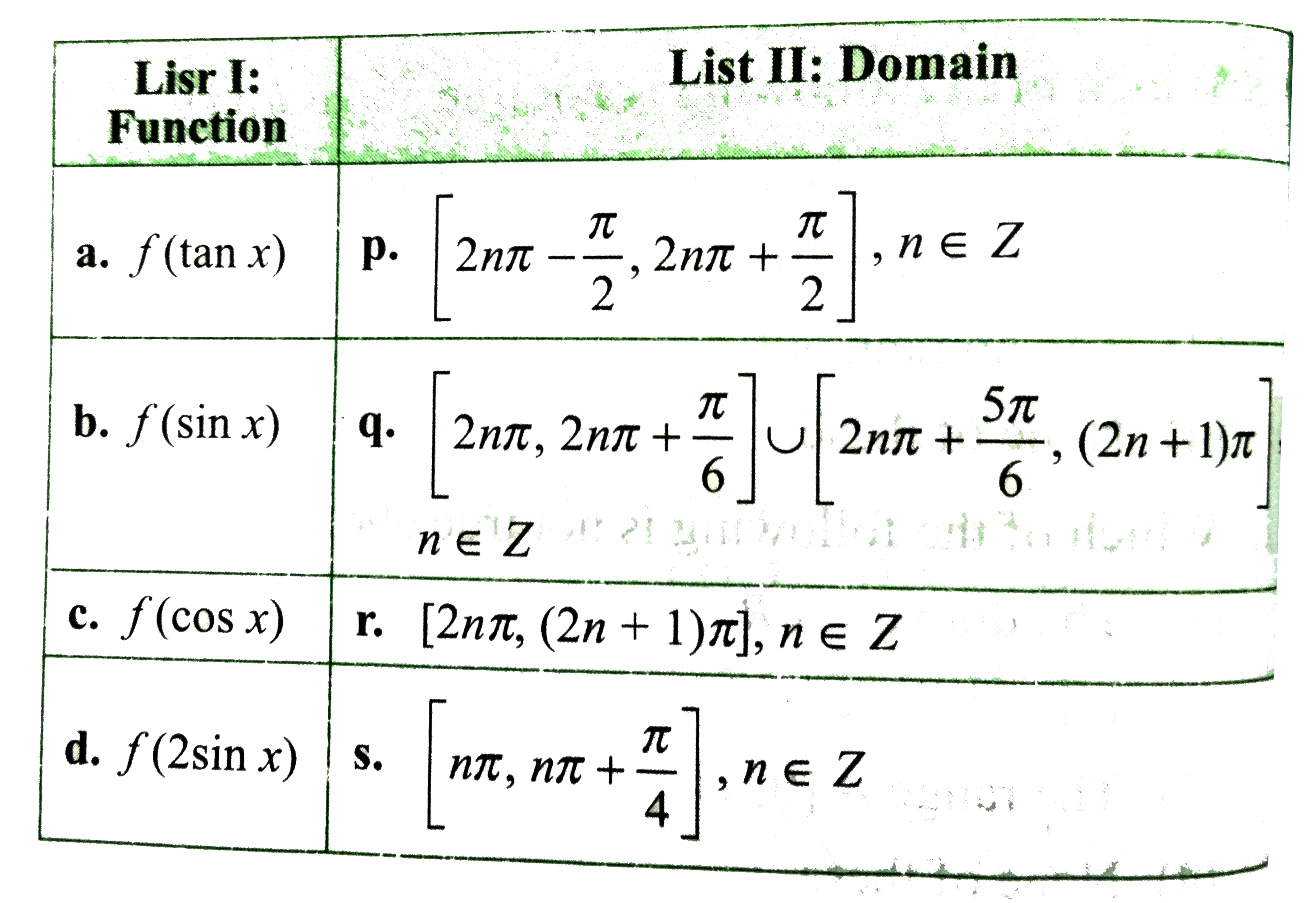
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionSuppose that f(x) is a function of the form f(x) =ax8+bx6+cx4+dx2+15x+1x,(x≠0).Iff(5)=2, then the value of |f(−5)|/4 is____
View SolutionA function f is differentiable in the interval 0
View SolutionIf f(4−x)=f(4+x) and f(8−x)=f(8+x) and f(x) is a function for which ∫80f(x)dx=5. Then ∫2000f(x)dx is equal to
View SolutionSuppose that f(x) is a function of the form
f(x)=ax8+bx6+cx4+dx2+15x+1x,(x≠0). If f(5)=2, then the value of f(−5) is _________.
View SolutionExamine the following functions for continuity. (a) f(x)=x−5 (b) f(x)=1x−5 (c) f(x)=x2−25x+5 (d) f(x)=|x−5|
View SolutionExamine the following functions for continuity.
(a) f(x)=x−5
(b) f(x)=1x−5
(c) f(x)=x2−25x+5
(d) f(x)=|x−5|
View SolutionSuppose that f(x) is a function of the form f(x) =ax8+bx6+cx4+dx2+15x+1x,(x≠0).Iff(5)=2, then the value of |f(−5)|/4 is____
View SolutionSuppose ∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0 is continuously differentiable function with f′(x)≠0 and satisfies f(0)=1 and f'(0)=2 then (lim)x→0f(x)−1x is 1/2 b. 1 c. 2 d. 0
View SolutionSuppose that f(x) is a function of the form
f(x)=ax8+bx6+cx4+dx2+15x+1x,(x≠0). If f(5)=2, then the value of f(−5) is _________.
View SolutionIf f(x)=ax2+bx+c is a quadratic function such that f(1)=8,f(2)=11 and f(−3)=6 find f(x) by using determinants. Also, find f(0).
View Solutionagreed f(x)=(ax^(8)+bx^(6)+cx^(4)+dx^(2)+15x+1)/x(x!=0 As a function if f(5)=2 , Then |f(-5)|//4 The value of
View Solutionagreed f(x)=(ax^(8)+bx^(6)+cx^(4)+dx^(2)+15x+1)/x(x!=0) As a function if f(5)=2 Then |f(-5)|//4 The value of
View Solution
