The function f(x)=x+1x3+1 can be written as the sum of an even function g(x) and an odd function h(x) . Then the value of |g(0)| is___________Solution in Tamil
The correct Answer is:0
g(x)=f(x)+f(−x)2
=12[x+1x3+1+1−x1−x3]
=12[1x2−x+1+11+x+x2]
=12[2(x2+1)(x2+1)2−x2]
=x2+1x4+x2+1
∴g(0)=1
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year
12 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
For real x, let f(x)=x3+5x+1 , then (1) f is oneone but not onto R (2) f is onto R but not oneone (3) f is oneone and onto R (4) f is neither oneone nor onto R
View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
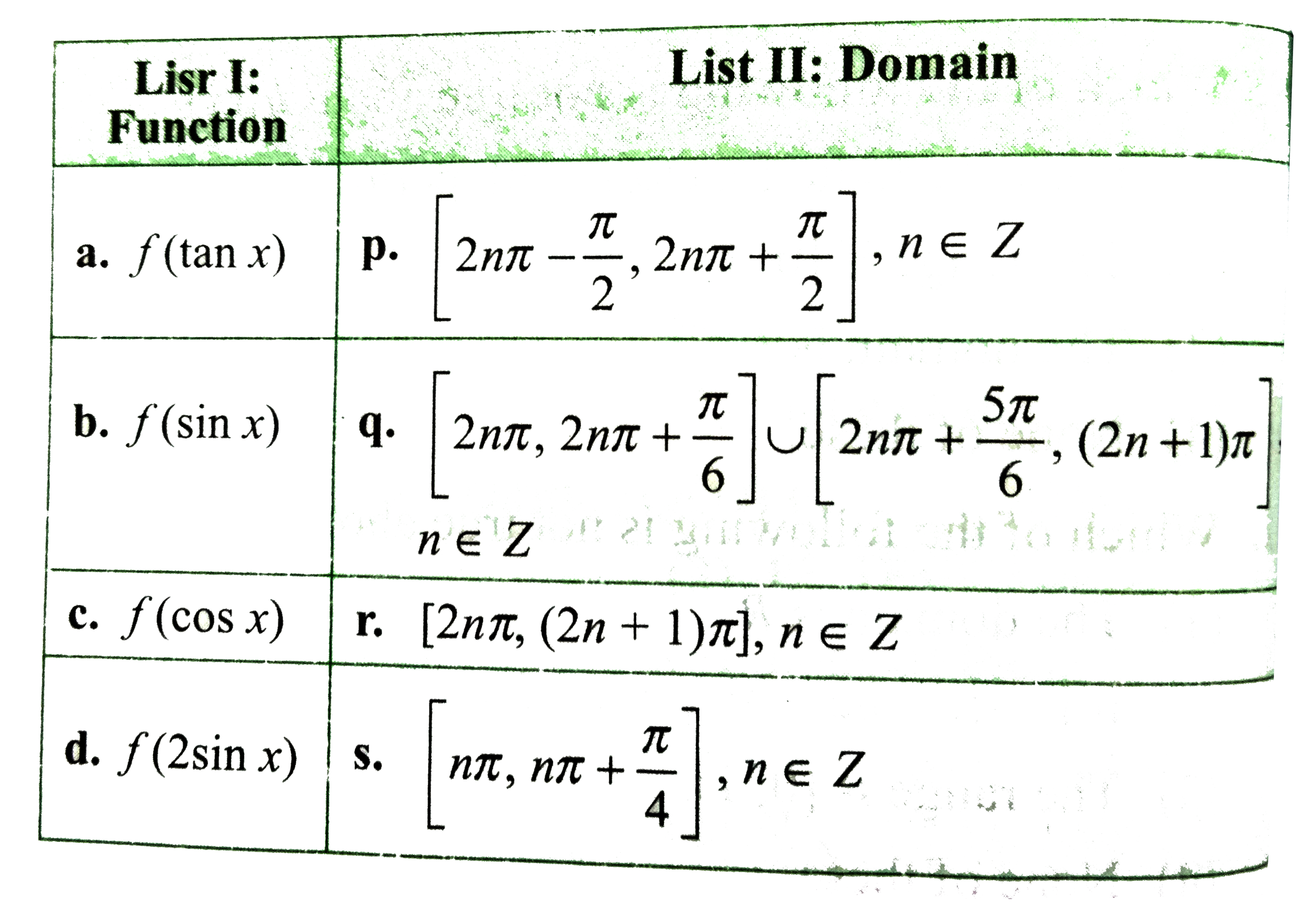
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionThe function f(x)=x+1x3+1 can be written as the sum of an even function g(x) and an odd function h(x) . Then the value of |g(0)| is___________
View SolutionLet f be a differential function such that f(x)=f(2-x) and g(x)=f(1+x) then (1) g(x) is an odd function (2)g(x) is an even function (3) graph of f(x) is symmetrical about the line x=1 (4) f'(1)=0
View SolutionLet f(x)=|x-2|+|x-3|+|x-4| and g(x)=f(x+1). Then 1.g(x) is an even function 2.g(x) is an odd function 3.g(x) is neither even nor odd 4.g(x) is periodic
View SolutionStatement I The function f(x)=∫x0√1+t2dt is an odd function and g(x)=f'(x) is an even function , then f(x) is an odd function.
View SolutionLet f(x)=ax(a>0) be written as f(x)=g(x)+h(x) where g(x) is an even function and h(x) is an odd function. Then the value of g(x+y)+g(x−y) is -
View SolutionIf f(x)andg(x) are two functions such that f(x)+g(x)=exandf(x)−g(x)=e−x then
I: f(x) is an even function
II : g(x) is an odd function
III : Both f(x) and g(x) are neigher even nor odd.
View SolutionAssertion: The product of even functions an odd function is an odd function.
Reason: f(x)=x2 is even function, g(x)= an odd function.
View SolutionThe function f(x)=x+1x3+1 can be written as the sum of an even function g(x) and an odd function h(x) . Then the value of |g(0)| is___________
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionThe function f(x)=x+1x3+1 can be written as the sum of an even function g(x) and an odd function h(x) . Then the value of |g(0)| is___________
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionIf f(x) is an even function and g(x) is an odd function and satisfies the relation x2f(x)−2f(1x)=g(x) then
View Solution
