f(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
Which of the following is not true about h1(x)?Solution in Tamil
It is a periodic function with period π.
The range is [0, 1].
The domain is R.
None of these
The correct Answer is:D
|g(x)|=|sinx|,x∈R
f(|g(x)|)={|sinx|−1,−1≤|sinx|<0(|sinx|)2,0≤(|sinx|)≤1=sin2x,x∈R
f(g(x))={sinx−1,−1≤sinx<0sin2x,0≤sinx≤1
={sinx−1,(2n−1)π<x<2nπsin2x,2nπ≤x≤(2n+1)π,n∈Z.
or |f(g(x))|={sinx−1,(2n−1)π<x<2nπsin2x,2nπ≤x≤(2n+1)π,n∈Z.
Clearly, h1(x)=f(|g(x)|)=sin2x has period π, range [0, 1], and domain R.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)
31 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)
27 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
The function f(x) is defined on the interval [0, 1]. Now, match the following lists:
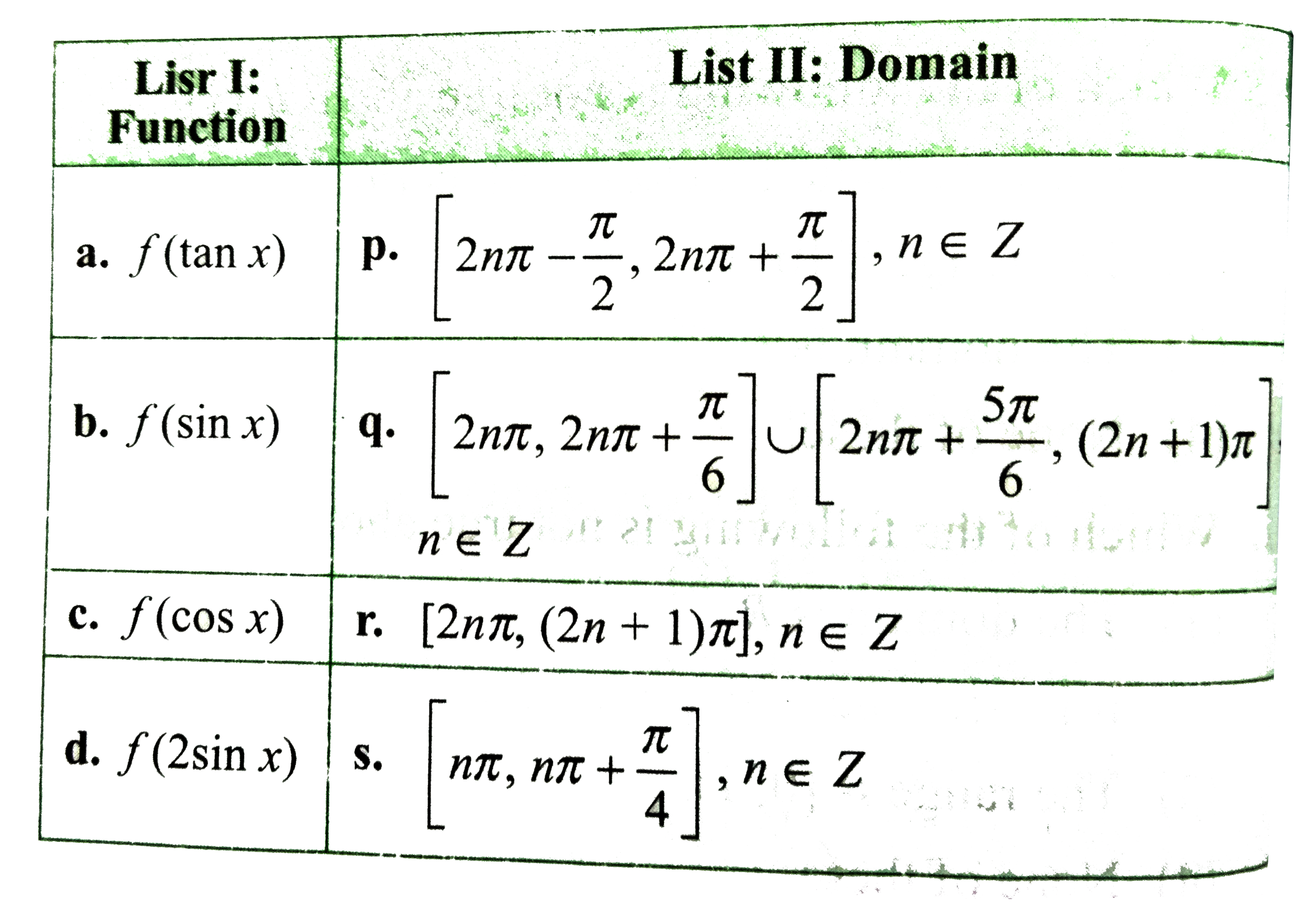
View SolutionLet f be a real-valued invertible function such that f(−32xx−2)=5x−2,x≠2. Then value of f−1(13) is________
View SolutionLet f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the range of f(x) is
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionThe relation f is defined by f(x)={3x+2, 0≤x≤2x3, 2≤x≤5.
The relation g is defined by g(x)={3x+2, 0≤x≤1x3, 1≤x≤5
Show that f is a function and g is not a function
View SolutionConsider the functions
f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
The domain of the function f(g(x)) is
View Solutionf(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
If for h1(x)andh2(x) are identical functions, then which of the following is not true?
View SolutionLet f(x) and g(x) be two functions given by f(x)=−1|x−1|,−1≤x≤3 and g(x)=2−|x+1|,−2≤x≤2
Then,
View SolutionLet f(x)=x3−x2+x+1andg(x) be a function defined by g(x)={Max{f(t):0≤t≤x}0≤x≤13−x1≤x≤2 Then, g(x) is
View SolutionConsider the function f(x)=f(x)={x−1,−1≤x≤0x2,0≤x≤1
and g(x)=sinx.
If h1(x)=f(|g(x)|)
and h2(x)=|f(g(x))|.
Which of the following is not true about h1(x)?
View SolutionConsider the function f(x)=f(x)={x−1,−1≤x≤0x2,0≤x≤1
and g(x)=sinx.
If h1(x)=f(|g(x)|)
and h2(x)=|f(g(x))|.
Which of the following is not true about h2(x)?
View SolutionLet f(x)=−x3+x2−x+1andg(x)={min(f(t)),0≤t≤xand0≤x≤1x−1,1<x≤2 Then, the value of limx→1g(g(x)), is........ .
View Solutionमाना f(x)=x3−x2+x+1 और g(x)={max{f(t),0≤t≤x}0≤x≤13−x1<x≤2
फलन g(x) की सततता तथा अवकलनीयता अंतराल (0, 2) पर ज्ञात कीजिए |
View Solutionमाना {−1,−2≤x≤0x2−1,0≤x≤2 तथा g(x)=|f(x)|+f(|x|) तो अंतराल (-2, 2), में फलन g
View SolutionIf the function f(x)={x+1 if x≤1 , 2x+1 if 1<x≤2 and g(x)={x2 if −1≤x≤2, x+2if2≤x≤3 then the number of roots of the equation f(g(x))=2
View Solution
