Let f:R→R is a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x),∀x∈R. On the basis of above information, answer the following questions If f(0)=5, then minimum possible number of values of x satisfying f(x)=5, for x∈[10,170] isSolution in Tamil
21
12
11
22
The correct Answer is:C
f(2−x)=f(2+x) (1)
Replace x by 2−x. Then f(x)=f(4−x) (2)
Also, given f(20−x)=f(x) (3)
From (1) and (2), f(4−x)=f(20−x).
Replace x by 4−x. Then f(x)=f(x+16).
Hence, the period of f(x) is 16.
Given f(0)=5.
∴f(0)=f(16)=f(32)=...=f(160)=5
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Exercise (Matrix)
Explore 9 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Exercise (Numerical)
Explore 31 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Exercise (Multiple)
Explore 27 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBook:CENGAGEChapter:Quadratic Equations, Inequalities, Modulus and LogarithmsExercise:Question Bank
Explore 28 Videos
- SCALER TRIPLE PRODUCTS Book:CENGAGEChapter:SCALER TRIPLE PRODUCTS Exercise:DPP 2.3
Explore 11 Videos
Similar Questions
The function f(x) is defined on the interval [0, 1]. Now, match the following lists:
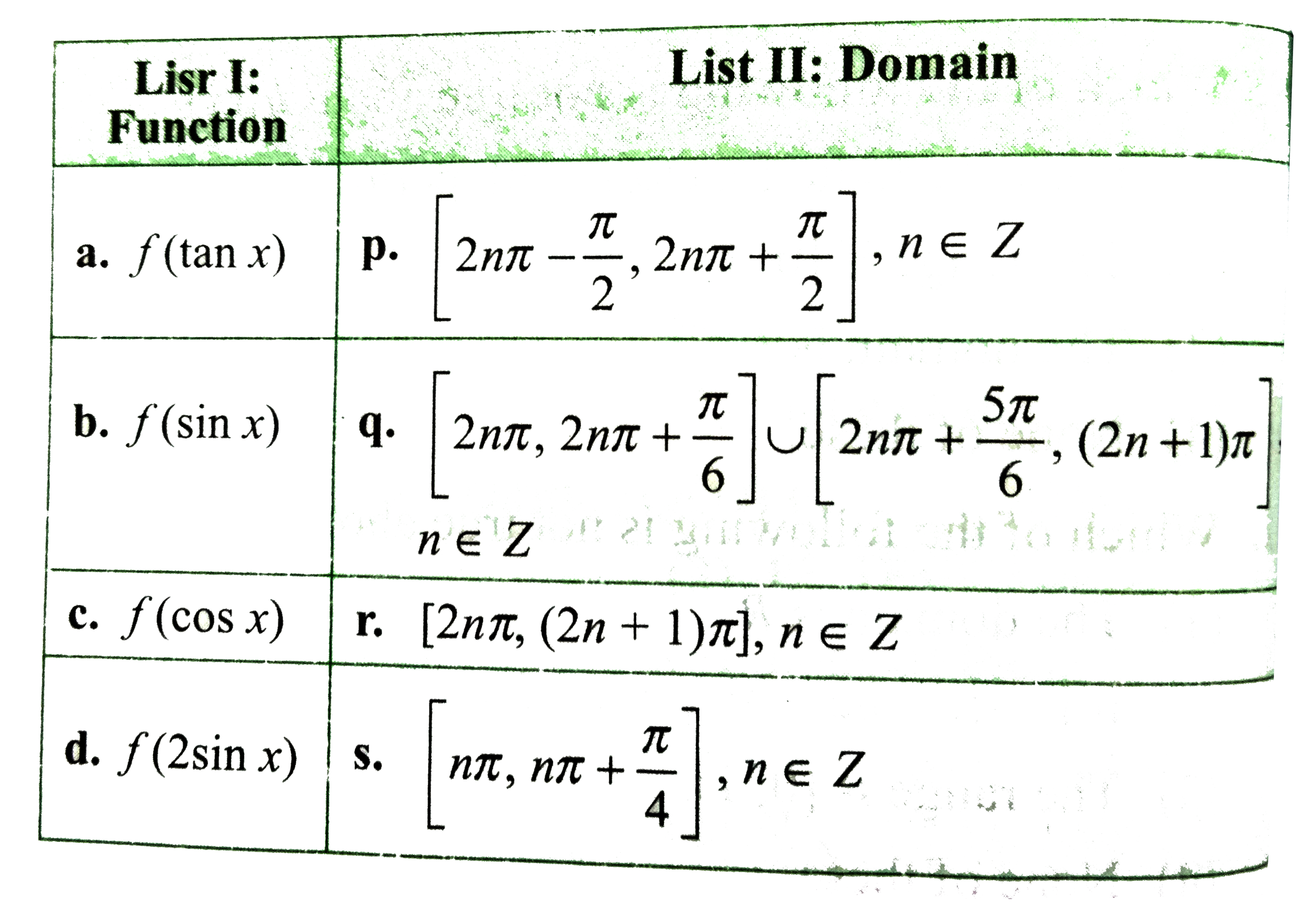
View SolutionLet f be a real-valued invertible function such that f(−32xx−2)=5x−2,x≠2. Then value of f−1(13) is________
View SolutionLet f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the range of f(x) is
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionLet a real valued function f satisfy f(x+y)=f(x)f(y)∀x,y∈Randf(0)≠0 Then g(x)=f(x)1+[f(x)]2 is
View SolutionA function f:R rarr R^(+) satisfies f(x+y)=f(x)f(y)AA x in R If f'(0)=2 then f'(x)=
View SolutionLet f(x) be a function satisfying f(x)f(x+2)=10∀x∈R, then
View SolutionIf a function satisfies the relation f(x)f''(x)−f(x)f'(x)=(f'(x))2∀x∈Randf(0)=f'(0)=1, then
The value of limx→−∞f(x) is
View SolutionLet f:R→R be a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x)∀x∈R. For this function f, answer the following.
If f(2)≠f(6), then the
View SolutionA function f : R→R Satisfies the following conditions
(i) f(x)≠0∀x∈R
(ii) f(x+y)=f(x)f(y)∀x,y,∈R
(iii) f(x) is differentiable
(iv ) f'(0) =2
The derivative of f(x) satisfies the equation
View SolutionLet f(x) be a continuous & differentiable function on R satisfying f(−x)=f(x)&f(3+x)=f(3−x)∀x∈R. If f'(1)=−5 then f'(7) =
View SolutionLet f:R→R is a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x),∀x∈R. On the basis of above information, answer the following questions If f(0)=5, then minimum possible number of values of x satisfying f(x)=5, for x∈[10,170] is
View SolutionLet f:R→R be a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x)∀x∈R. For this function f, answer the following.
If f(2)≠f(6), then the
View SolutionLet f:R→R be a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x)∀x∈R.For this functions f. answer the following
The graph of y = f(x) is not symmetrical about
View Solution