Consider the function f(x) satisfying the identity f(x)+f(x−1x)=1+x∀x∈R−{0,1},andg(x)=2f(x)−x+1.
The domain of y=√g(x) is Solution in Tamil
(−∞,1−√52]∪[1,1+√52]
(−∞,1−√52]∪(0,1)∪[1+√52,∞)
[−1−√52,0]∪[−1+√52,1)
None of these
The correct Answer is:B
f(x)+f(x−1x)=1+x (1)
In (1), replace x by x−1x. Then
f(x−1x)+f⎛⎝x−1x−1x−1x⎞⎠=1+x−1x
orf(x−1x)+f(11−x)=1+x−1x (2)
Now, from (1)−(2), we have
f(x)−f(11−x)=x−x−1x (3)
In (3), replace x by 1x−1. Then
f(11−x)−f(x−1x)=11−x−11−x−111−x
orf(11−x)−f(x−1x)=11−x−x (4)
Now, from (1)+(3)+(4), we have
2f(x)=1+x+x−x−1x+11−x−x
orf(x)=x3−x2−12x(x−1)
g(x)=x3−x2−1x(x−1)−x+1=x2−x−1x(x−1)
Now, for y=√g(x), we must have x2−x−1x(x−1)≥0
or(x−1−√52)(x−1+√52)x(x−1)≥0
orx∈(−∞,1−√52]∪(0,1)∪[1+√52,∞)
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)
31 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)
27 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
The function f(x) is defined on the interval [0, 1]. Now, match the following lists:
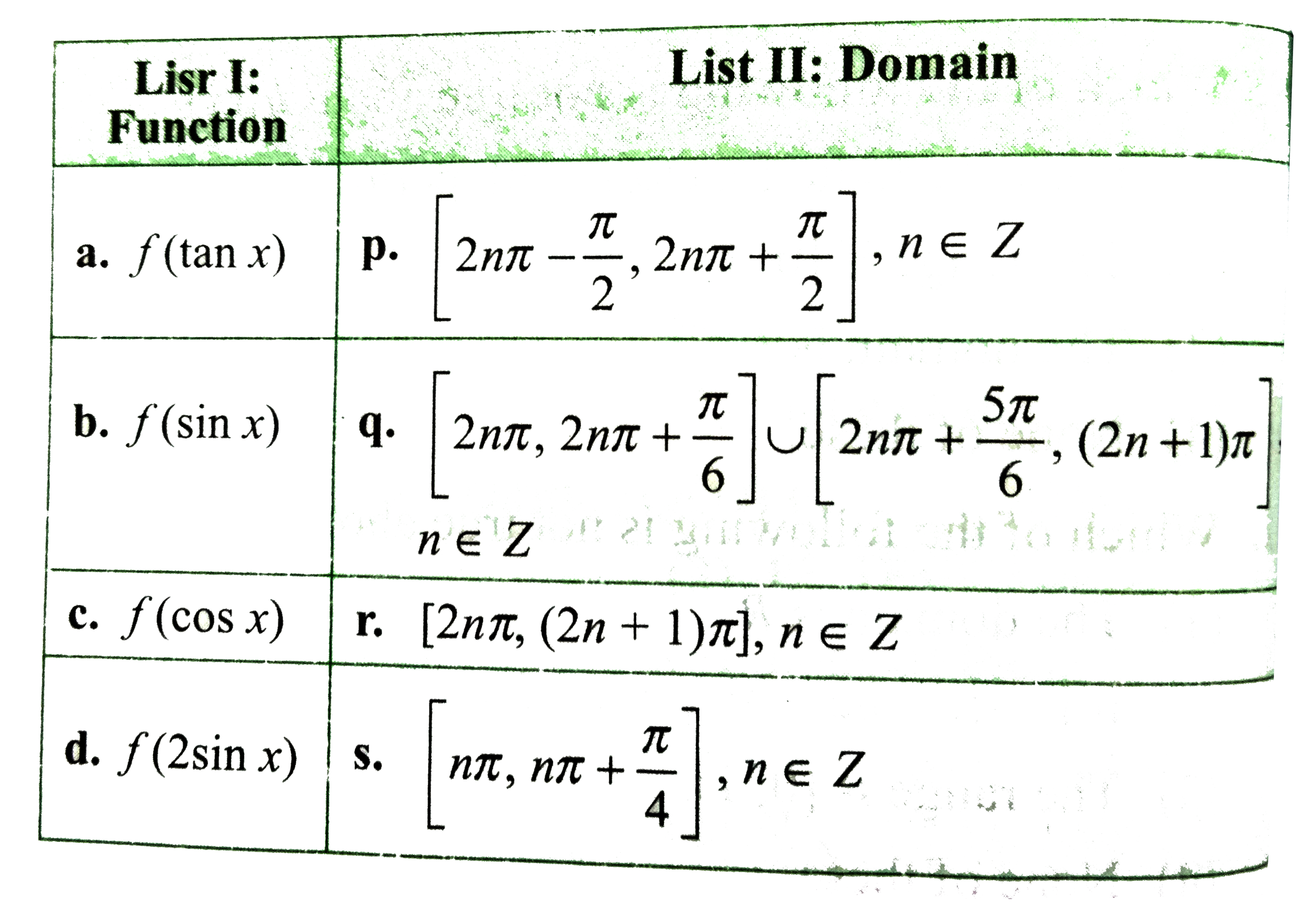
View SolutionLet f be a real-valued invertible function such that f(−32xx−2)=5x−2,x≠2. Then value of f−1(13) is________
View SolutionLet f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the range of f(x) is
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionConsider the function f(x) satisfyig the identity f(x)+f((x-1)/(x))=1+x,AA x in R-{0,1} and g(x)=2f(x)-x+1
View SolutionLet a real valued function f satisfy f(x+y)=f(x)f(y)∀x,y∈Randf(0)≠0 Then g(x)=f(x)1+[f(x)]2 is
View SolutionConsider the function f(x) satisfying the identity f(x)+f(x−1x)=1+x∀x∈R−{0,1},andg(x)=2f(x)−x+1.
The domain of y=√g(x) is
View SolutionThe function f(x) satisfy the equation f(1−x)+2f(x)=3x∀x∈R, then f(0)=
View SolutionIf f(x)=1+1/x,g(x)=√1−x2 , then the domain of f(x)−g(x) is
View SolutionFind all functions f satisfying the identity, f(x)+f(x−1x)=1+x,∀x∈R−{0,1}
View SolutionLet f be a continuous function on R satisfying f(x+y)=f(x)+f(y) for all x,y∈R with f(1)=2andg be a function satisfying f(x)+g(x)=ex then the value of the integral ∫10f(x)g(x)dx is
View SolutionConsider the function f(x) satisfying the identity f(x)+f(x−1x)=1+x∀x∈R−{0,1},andg(x)=2f(x)−x+1.
The domain of y=√g(x) is
View SolutionConsider the function f(x) satisfyig the identity f(x)+f(x−1x)=1+x,∀x∈R−{0,1} and g(x)=2f(x)−x+1 Then range of y=g(x) is:
View SolutionIf f(x) is an even function and g(x) is an odd function and satisfies the relation x2f(x)−2f(1x)=g(x) then
View Solution
