If x∈[1,2] , then find the range of f(x)=tanxSolution in Tamil
The correct Answer is:(−∞,tan2]∪[tan1,∞)
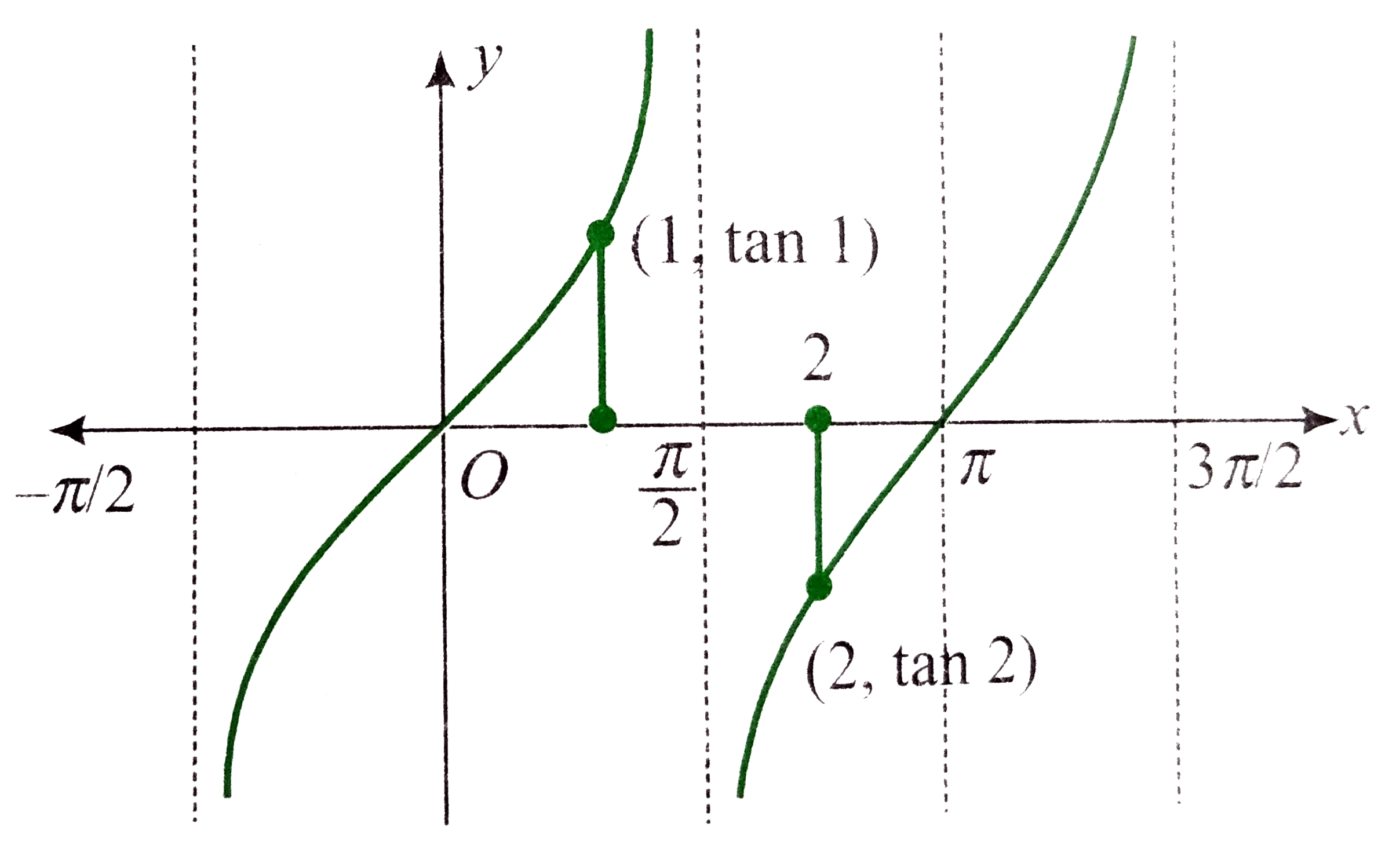
f(x)=tanx,x∈[1,2]
Here, the limited values of x are given.
The best way to get the range of tanx for such values of x is graphical one.
Consider the graph of f(x)=tanx for x∈[1,2].
Clearly, from the graph, tan∈(−∞,tan2]∪[tan1,∞).
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.7
5 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.8
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.5
5 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Find the domain of the following following functions:
(a) f(x)=sin−1x
(b) f(x)=sin−1(|x−1|−2)
(c ) f(x)=cos−1(1+3x+2x2)
(d ) f(x)=sin−1(x−3)√9−x2
(e ) f(x)=cos−1(6−3x4)+cosec−1(x−12)
(f) f(x)= ⎷sec−1(2−|x|4)
View SolutionFind the domain of the function : f(x)=√4x+8(23)(2x−2)−13−22(x−1)
View SolutionThe entire graph of the equation y=x2+kx−x+9 in strictly above the x−aξs if and only if k<7 (b) −5<k<7 k≻5 (d) none of these
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionA function f has domain [−1,2] and rang [0,1] . Find the domain and range of the function g defined by g(x)=1−f(x+1).
View SolutionIf x∈[1,2] , then find the range of f(x)=tanx
View SolutionIf f(x)=ln(x^(2)-x+2);R^(+)rarr R and g(x)={x}+1;[1,2]rarr[1,2], Find the domain and range of f(g(x)) when defined.
View SolutionFind the derivative of f(x)=tanx at x=0.
View SolutionFind the range of f(x) =sinxx+xtanx∈(0,π2)
View Solutionf(x)=tanx का x=0 पर अवकलज ज्ञात कीजिए ।
View SolutionFind f'(x) if f(x)=(tanx)tanx
View SolutionIf f(x)=(x+cosx)(x−tanx), find f′(x).
View SolutionFind f'(x) if f(x)=(tanx)tanx
View SolutionA function f has domain [−1,2] and range [0,1] . Find the domain and range of the function g defined by g(x)=1−f(x+1).
View SolutionIf x∈[1,2] , then find the range of f(x)=tanx
View Solution
