Question

Prove that the least positive value of ${\displaystyle x,}$
satisfying ${\displaystyle \tan x=x+1,}$
lies in the interval ${\displaystyle (\frac{\pi }{4},\frac{\pi }{2})}$

Explanation

Let `f(x)=tan x " and " g(x)=x+1,` which can be shown as follows.

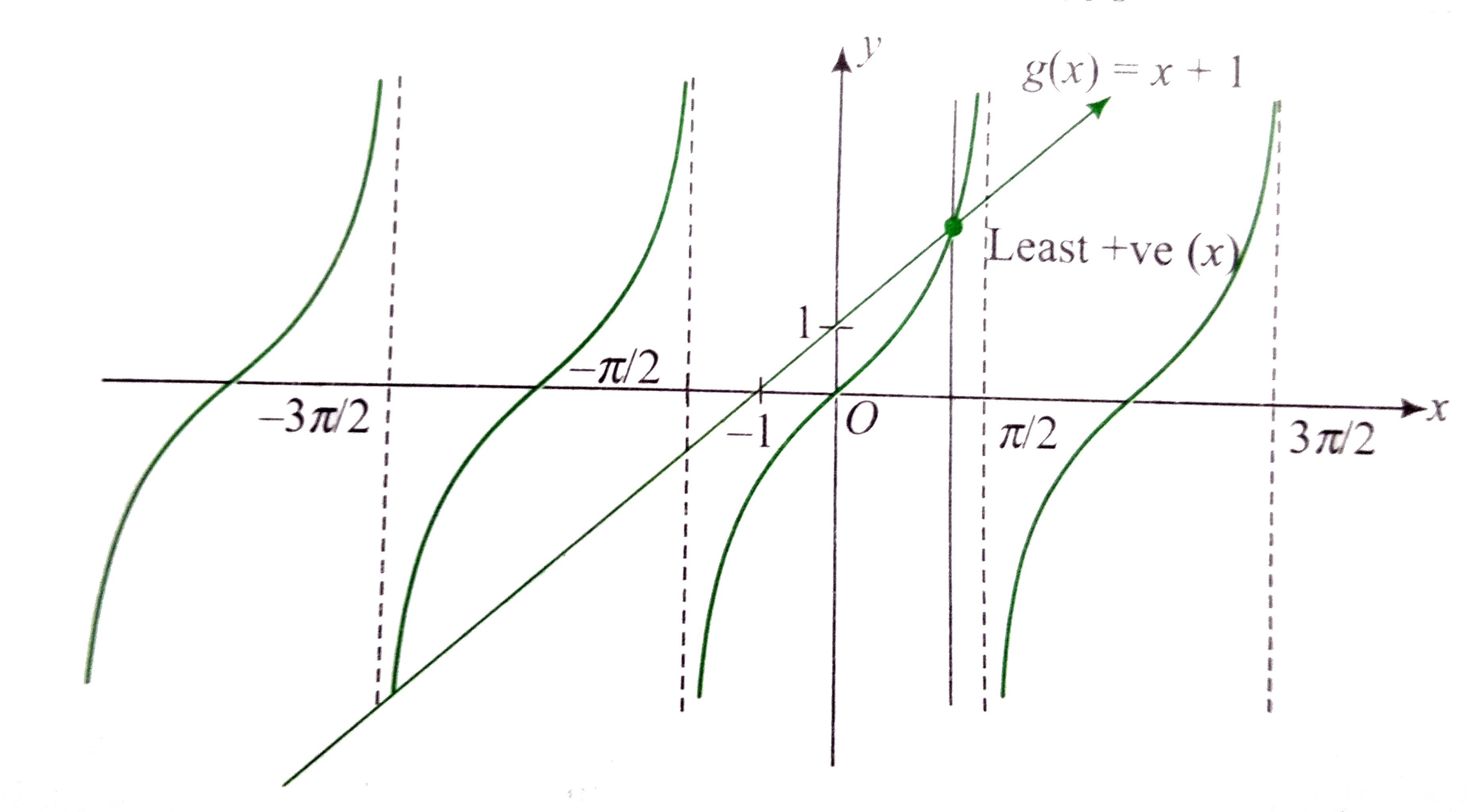
From the figure, `tanx =x+1` has infinitely many solutions but the least positive value of x lies in `((pi)/(4),(pi)/(2)).`