Let f(x)=sin6x+cos6x+k(sin4x+cos4x) for some real number k. Value of k for which f(x) is constant for all values of x is −12 (b) 12 (c) 14 (d) −32 All real numbers k for which the equation f(x)=0 has solution lie in [−1,0] (b) [0,12] (c) [−1,−12] (d) none of these Number of values of k for which f(x)=0 is an identity is (a) 0 (b) 1 (c) infinite (d) none of theseSolution in Tamil
0
1
infinite
None of these
The correct Answer is:A
(1−3sin2xcos2x)+k[1−2sin2xcos2x]=0 is an identity,
i.e., (1+k)−(3+2k)sin2xcos2=0 is an identity.
⇒1+k=and3+2k=0, which do not hold simultaneously.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Matrix)
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Numerical)
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Multiple)
17 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
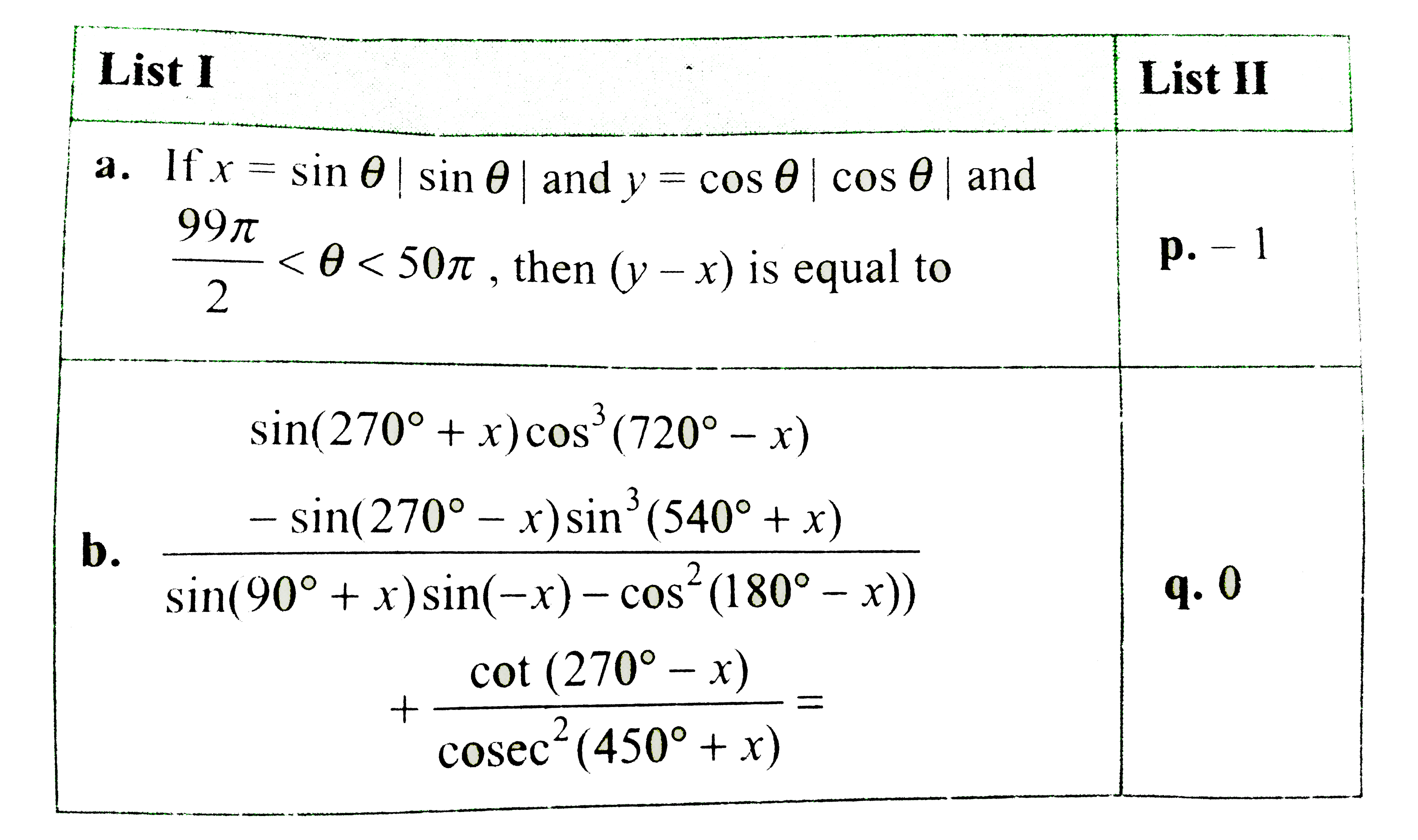
View SolutionThe value of the expression tan2200−sin2200tan2200+sin2200 is__________
View SolutionIf 0≤θ≤πand81sin2θ+81cos2θ=30 is
View SolutionFind the derivative of y=tan−12x3
View SolutionRefer to the following diagram :

Column IColumn IIa.Collinear vectorsp.→ab.Coinitial vectorsq.→bc.Equal vectorsr.→cd.Unlike vectors (same initial point)s.→d
View SolutionThe value of k which makes f(x)={sinxx,x≠0,andk,x=0 , continuous at x=0,is (a) 8 (b) 1 (c) −1 (d) none of these
View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
View SolutionLet f(x)=2x+1. Then the number of real number of real values of x for which the three unequal numbers f(x),f(2x),f(4x) are in G.P. is 1 b. 2 c. 0 d. none of these
View SolutionThe jump value of the function at the point of the discontinuity of the function f(x)=(1-k^(1/x))/(1+k^(1/x))(k>0) (k=1) is: (A) 4 (B) 2 (C) 3 (D) None of these
View SolutionIf the equation sin x+cos(k+x)+cos(k-x)=2 has real solutions,then sin k can be(A)(1)/(4)(B)(1)/(sqrt(2))(C)(3)/(4)(D)-(3)/(4)
View SolutionLet f(x)=sin6x+cos6x+k(sin4x+cos4x) for some real number k. Determine all real numbers k for which f(x) is constant for all values of x.
View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
View SolutionThe number of value of k for which [x2−(k−2)x+k2]×[x2+kx+(2k−1)] is a perfect square is a.2 b. 1 c. 0 d. none of these
View SolutionLet f(x)=sin6x+cos6x+k(sin4x+cos4x) for some real number k. Determine(a) all real numbers k for which f(x) is constant for all values of x.
View SolutionThe value of k, for which
(cosx+sinx)2+ksinxcosx−1=0 is an identity, is ............ (A)2(B)−2(C)0(D)1
View SolutionLet f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2
View Solution
